Grundlagen - Induktivität und Kapazität

Elektromagnetismus

Elektrizität und Magnetismus sind untrennbar miteinander verbunden, wie schon der Begriff vermuten lässt. Der erste Merksatz dazu lautet:

Jeder stromdurchflossene Leiter ist von einem Magnetfeld umgeben.

Die Magnetfeldlinien sind kreisförmig um den Leiter herum angeordnet. Eine Kompassnadel in der Nähe dieses Leiters richtet sich in Richtung der magnetischen Feldlinien tangential zum Leiter aus.

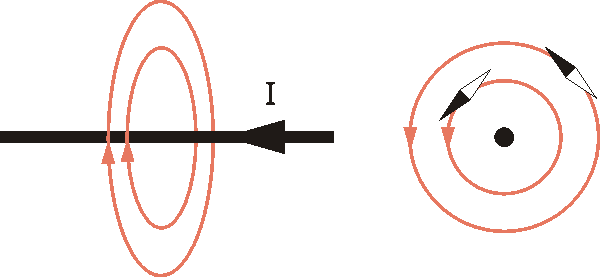
Die Stärke des Magnetfeldes erhöht sich mit steigender Stromstärke. Mit der Entfernung zum Leiter nimmt das Magnetfeld ab. Die magnetische Feldstärke H außerhalb eines stromdurchflossenen Leiters beträgt $$H = \frac{I}{2 \pi \cdot r}.$$ r ist dabei der Radius der Magnetfeldlinie, also der Abstand zum Leiter. Es gibt aber noch einen zweiten Zusammenhang zwischen beiden Phänomenen.

Wird ein elektrischer Leiter in einem Magnetfeld bewegt oder ändert sich um einen feststehenden Leiter die Stärke des Magnetfeldes, entsteht an seinen Enden eine elektrische Spannung.

Dieser Vorgang wird Induktion genannt. Die induzierte Spannung ist davon abhängig, wie stark und wie schnell sich der magnetische Fluss Φ ändert. $$U_{ind} = - \frac{\Delta \Phi}{\Delta t}$$ Die induzierte Spannung lässt sich vervielfachen, wenn man den Leiter zu einer Spule aufwickelt. In dem Fall multipliziert man die Formel mit der Windungszahl N. Der Effekt lässt sich weiter verstärken, wenn man ein gut magnetisierbares Material in den Kern der Spule bringt. Die Fähigkeit zur Induktion beschreibt man mit der Größe Induktivität L in Henry (H). Ändert sich innerhalb einer Sekunde die Stromstärke um 1A, dann erzeugt eine Spule mit 1H eine Induktionsspannung von 1V. Ähnlich wie beim elektrischen Widerstand lässt sich die Induktivität einer Spule aus der Geometrie und den Materialkonstanten berechnen, allerdings nicht ganz so einfach und nicht so genau. Für eine einlagige Zylinderspule gilt: $$L = μ_0 \cdot μ_r \cdot \frac{N^2 \cdot A}{l} \cdot k$$ Die Induktionskonstante μ₀ ist eine Naturkonstante, die das Verhältnis der magnetischen Flussdichte zur magnetischen Feldstärke im Vakuum angibt = $4 π \cdot 10^{-7} \frac{Vs}{Am}$.
Die relative Permeabilität μ_r ist die Materialkonstante des Spulenkerns.
N ist die Windungszahl, A der Spulenquerschnitt und l die Spulenlänge.
Der Korrekturfaktor k ist abhängig vom Verhältnis des Durchmessers der Spule zu deren Länge und lässt sich aus der Tabelle im Anhang ablesen.

Die Spule im Stromkreis

Während sich an einem rein ohmschen Widerstand der Strom zeitgleich mit der angelegten Spannung ändert, verhält sich eine Spule etwas anders. Betrachten wir zuerst die Verhältnisse in einem Gleichstromkreis.
Im Einschaltmoment erzeugt der einsetzende Strom in der Spule ein ansteigendes Magnetfeld. Dieses induziert in der Spule eine Spannung, welche der angelegten Spannung entgegengerichtet ist und so den Stromfluss bremst. Der Strom steigt also erst allmählich auf seinen maximalen Wert an.

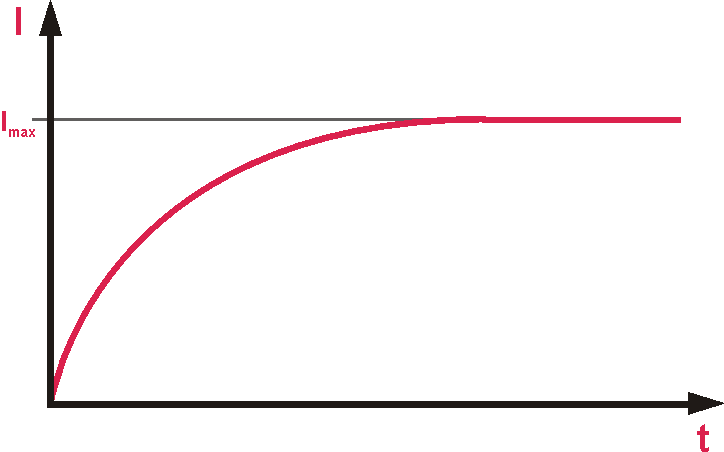
Man kann auch sagen, die Spule setzt dem Strom anfangs einen sehr hohen Widerstand entgegen, der mit der Zeit abnimmt. Hat der Strom sein Maximum erreicht, wird er nur noch durch den ohmschen Widerstand des Spulendrahtes begrenzt.
Trennt man den Stromkreis wieder auf, bricht das Magnetfeld der Spule fast schlagartig zusammen. Wegen der schnellen Magnetfeldänderung entsteht gemäß dem Induktionsgesetz an der Spule eine sehr hohe Induktionsspannung, die zu einem Lichtbogen am Schalter führt. Würde man jetzt die Spule nach dem Trennen von der Spannungsquelle mit einem Widerstand verbinden, würde der Strom so lange weiterfließen, bis das Magnetfeld der Spule völlig abgebaut ist.

Interessanter wird das Verhalten im Wechselstromkreis, wo sich die Spannung ständig verändert. Durch die Selbstinduktion der Spule folgt der Strom dem Spannungsverlauf zeitversetzt um ¼ Periode. Der Strom hinkt der Spannung um 90° hinterher, oder anders betrachtet, die Spannung eilt dem Strom um 90° voraus.

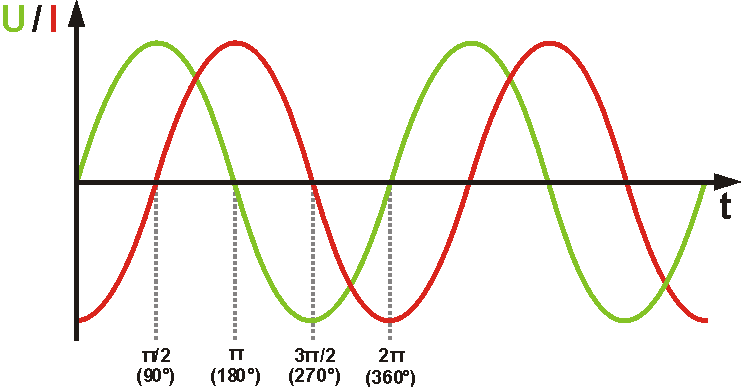
Der Widerstand einer Spule im Wechselstromkreis setzt sich aus zwei Komponenten zusammen, dem ohmschen Widerstand R des Spulendrahtes und einem Teil, der nur im Wechselstromkreis wirksam wird. Man nennt diesen Teil auch Blindwiderstand, da an ihm die elektrische Energie nicht "verbraucht" wird, d.h. nicht in andere Energieformen umgewandelt wird. Die Größe des induktiven Blindwiderstandes hängt ab von der Induktivität der Spule und der Frequenz der Wechselspannung. $$X_L = 2π \cdot f \cdot L = ω \cdot L$$ Das Produkt $2π \cdot f$ nennt man auch Kreis- oder Winkelfrequenz ω. Wie die Frequenz ist auch sie ein Maß für die Schnelligkeit der Schwingung, allerdings nicht bezogen auf die Anzahl der Schwingungen pro Sekunde, sondern bezogen auf den überstrichenen Phasenwinkel.

Bei einer Reihenschaltung mehrerer Spulen addieren sich die Induktivitäten und damit auch die Blindwiderstände, vorausgesetzt die Magnetfelder der einzelnen Spulen beeinflussen sich nicht gegenseitig. $$L_{ges} = L_1 + L_2 + L_3 + ...$$ Bei parallel geschalteten Spulen berechnet sich die resultierende Induktivität ähnlich wie bei der Parallelschaltung von ohmschen Widerständen. $$\frac{1}{L_{ges}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} + ...$$

Der Kondensator

Bringt man zwei elektrische Leiter mit unterschiedlicher Ladung nahe zusammen, beeinflussen sich die Ladungen gegenseitig. Die unterschiedlichen Ladungen halten sich quasi durch ihre Anziehung gegenseitig fest. Diesen Effekt kann man nutzen, um elektrische Ladungsenergie zu speichern. Das entsprechende Bauelement nennt man Kondensator.

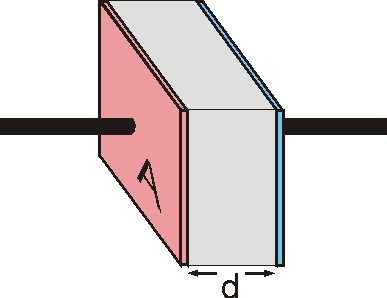
In der einfachsten Form sind das zwei Metallplatten, deren Flächen sich gegenüberstehen, ein sogenannter Plattenkondensator. Die Fähigkeit Ladungen aufzunehmen wird mit der Größe Kapazität beschrieben. Sie gibt an, welche Ladungsmenge ein Kondensator bei einer bestimmten Spannung speichern kann. $$C= \frac{Q}{U}$$ Die Maßeinheit für die Kapazität C ist das Farad (F). Q ist die Ladungsmenge in Coulomb (C). Sie ist immer ein Vielfaches einer einzelnen Elementarladung (e = 1,602176634 · 10^-19 C).
Achtung! Auch wenn die Formel so aussieht, ist die Kapazität eines Kondensators nicht von der Spannung, sondern von seiner Konstruktion abhängig. Bei einer höheren Spannung können mehr Ladungen "festgehalten" werden, sodaß der Quotient aus Ladung und Spannung immer gleich bleibt.

Wovon hängt die Kapazität eines Kondensators ab? Eine größere Oberfläche der Kondensatorplatten kann mehr Ladungen aufnehmen. Auch eine Verringerung des Abstandes der Platten erhöht die Fähigkeit, Ladungen zu halten. Der dritte Einfluss auf die Kapazität ist der Stoff, der sich zwischen den Platten befindet, das sogenannte Dielektrikum. Aus dem Aufbau eines Plattenkondensators lässt sich seine Kapazität wie folgt berechnen: $$C = ε_0 \cdot ε_r \cdot \frac{A}{d}$$ Der Wert der Dielektrizitätskonstante des Vakuums ε₀ beträgt $8,8541878128 \cdot 10^{-12} \frac{C}{Vm}$. Die relative Dielektrizitätskonstante ε_r ist die Materialkonstante des Dielektrikums. A ist die Fläche der Kondensatorplatten und d deren Abstand voneinander.

Der Kondensator im Stromkreis

Zunächst sehen wir uns wieder an, was beim Anlegen einer Gleichspannung passiert. Der Kondensator lädt sich entsprechend der Polarität der Spannungsquelle auf. Es fließt also ein Strom von Ladungsträgern zwischen Spannungsquelle und Kondensator.

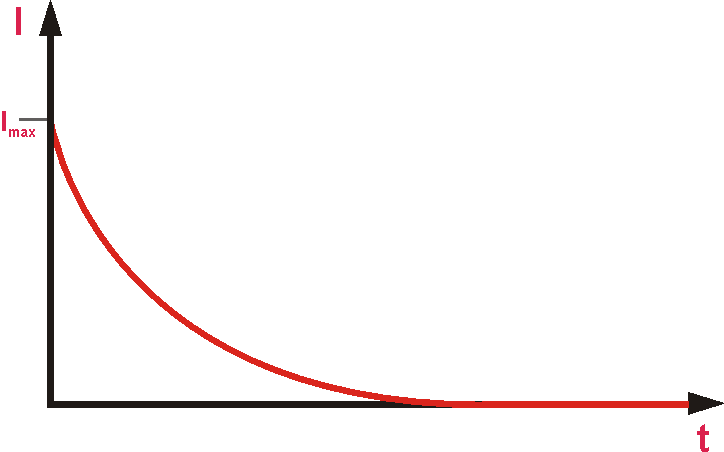
Obwohl die Kondensatorplatten voneinander isoliert sind, setzt der Kondensator anfangs dem Strom nur einen geringen Widerstand entgegen. Mit der Zeit sinkt der Ladestrom, um bei einem voll aufgeladenen Kondensator theoretisch auf 0 zu sinken. Jetzt wirkt der Kondensator wie ein Isolator.

Im Wechselstromkreis ändern sich Spannung und Polarität ständig. Der Kondensator wird nun ständig aufgeladen, entladen, in entgegengesetzter Richtung aufgeladen usw. Der Verlauf von Strom und Spannung ist wieder phasenverschoben. Der Strom eilt diesmal aber der Spannung um 90° voraus.

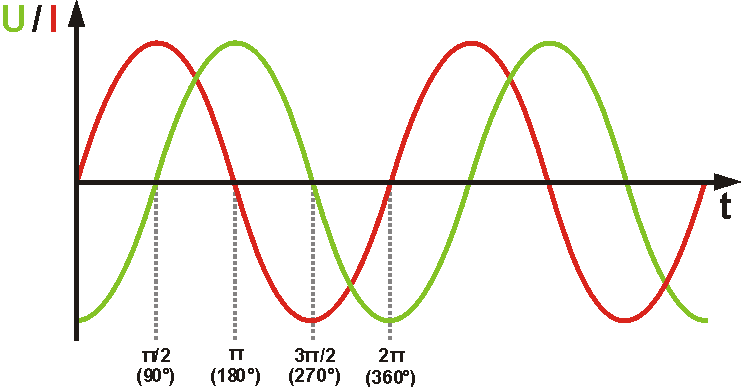
Da jetzt ständig ein Strom fließt, hat der Kondensator bei einer Wechselspannung einen endlichen Widerstand. Es handelt sich auch hier um einen Blindwiderstand, da der Strom ja nicht wirklich durch den Kondensator fließt. Auch der kapazitive Blindwiderstand ist abhängig von der Frequenz der Wechselspannung und natürlich von der Kapazität des Kondensators. Im Gegensatz zur Spule wird dieser allerdings mit steigender Frequenz kleiner. $$X_C = \frac{1}{ω \cdot C} = \frac{1}{2π \cdot f \cdot C}$$ Schaltet man mehrere Kondensatoren in Reihe, verringert sich die Gesamtkapazität der Schaltung. $$\frac{1}{C_{ges}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ...$$ Schaltet man mehrere Kondensatoren parallel, addieren sich die Kapazitäten. $$C_{ges} = C_1 + C_2 + C_3 + ...$$

Der Schwingkreis

Was passiert, wenn wir zwei so gegensätzlich arbeitende Bauelemente wie Spule und Kondensator zusammenbringen?
Beginnen wir mit einem voll aufgeladenen Kondensator. Wenn wir ihn mit einer Spule verbinden, fließt ein allmählich ansteigender Entladestrom und erzeugt ein Magnetfeld in der Spule.

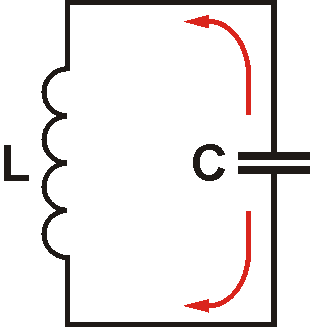
Wenn der Kondensator entladen ist, ist die Spannung gleich null und die gesamte Energie ist im Magnetfeld der Spule gespeichert, welches jetzt zusammenbricht und eine Induktionsspannung erzeugt, die den Strom weiterfließen lässt. Der Kondensator wird dadurch wieder aufgeladen, allerdings mit umgekehrter Polarität. Wenn die Spannung den maximalen Wert erreicht hat, ist der Ladestrom auf null gesunken. Jetzt beginnt der ganze Vorgang wieder von vorn, nur in umgekehrter Richtung.
Der Strom fließt also ständig im Stromkreis hin und her. Im Idealfall würde das jetzt auf ewig so weitergehen. Da wir es aber nicht mit idealen Bauelementen zu tun haben, wird ein Teil der Energie an den ohmschen Widerständen in Wärme umgewandelt. Es entsteht also eine gedämpfte Schwingung, die mit der Zeit nachlässt.

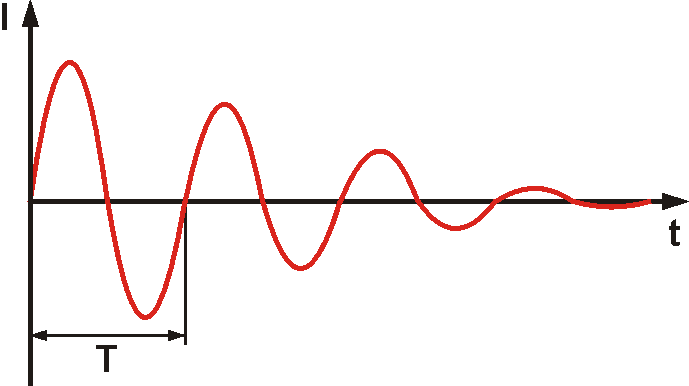
Die Länge einer Schwingung hängt von der Kapazität des Kondensators und der Induktivität der Spule ab. Je mehr Energie im Schwingkreis hin und her "geschaufelt" werden muss, je länger dauert eine Periode. Die Schwingungsdauer T ist also direkt proportional zur Kapazität und Induktivität. Die Frequenz der Schwingung ist der Kehrwert daraus und damit umgekehrt proportional zu L und C. Je größer C und L, je kleiner die Frequenz. $$T = 2π \cdot \sqrt{L \cdot C}$$ $$f = \frac{1}{T} = \frac{1}{2π \cdot \sqrt{L \cdot C}}$$ Wird der Schwingkreis im richtigen Takt "angeschubst", entsteht eine ungedämpfte Schwingung. So eine Schaltung nennt man Oszillator. Dazu benötigen wir Bauelemente, die Ströme bzw. Signale aktiv beeinflussen können. Die bisher behandelten Bauelemente Widerstände, Kondensatoren oder Spulen verhalten sich passiv im Stromkreis. Es ist Zeit, uns mit aktiven Bauelementen zu beschäftigen, die Ströme und Signale steuern oder verstärken können.

< vorige Seite <   > nächste Seite >