Karnaugh-Plan
Eine weitere Methode eine digitale Logik zu optimieren ist der sogenannte Karnaugh-Plan oder auch KV-Diagramm. Das KV-Diagramm ist eine etwas andere Darstellung einer Wahrheitstabelle. Die einzelnen Zellen zeigen den Zustand am Ausgang der Schaltung in Abhängigkeit von den logischen Pegeln an den verschiedenen Eingängen. Wie wird so ein Diagramm richtig aufgestellt? Die Größe des KV-Diagramms wird durch die Anzahl der Eingangswerte bestimmt, da alle Kombinationen dargestellt werden müssen. Wenn n die Anzahl der Eingänge ist, sind 2n Felder nötig.
In unserem Beispiel soll der Ausgang Y von den vier Eingangswerten A bis D abhängen. Wir brauchen also 24=16 Felder. Jede Zeile und Spalte steht für bestimmte Zustände an den Eingängen. Dabei steht zum Beispiel der Wert $A$ für eine 1 am Eingang und $\overline{A}$ für eine 0. Man muss die Zeilen und Spalten jetzt so zuordnen, dass sich in jeder Zelle eine andere Kombination von A bis D ergibt. In dem Feld mit dem blauen "Fadenkreuz" treffen sich die Werte $\overline{A},~ \overline{B},~ C~ und~ D$. Das entspricht den Werten ABCD = 0011.
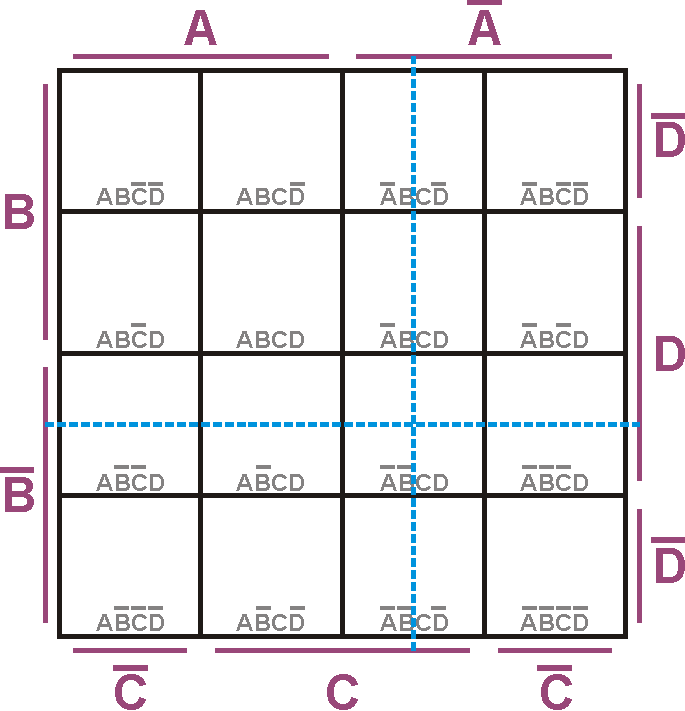
In die einzelnen Felder werden die entsprechenden Werte für Y aus der Wahrheitstabelle übernommen. Das rechte obere Feld entspricht der fünften Zeile und damit den Werten ABCD = 0100, was den Ausgang auf 1 setzen soll.
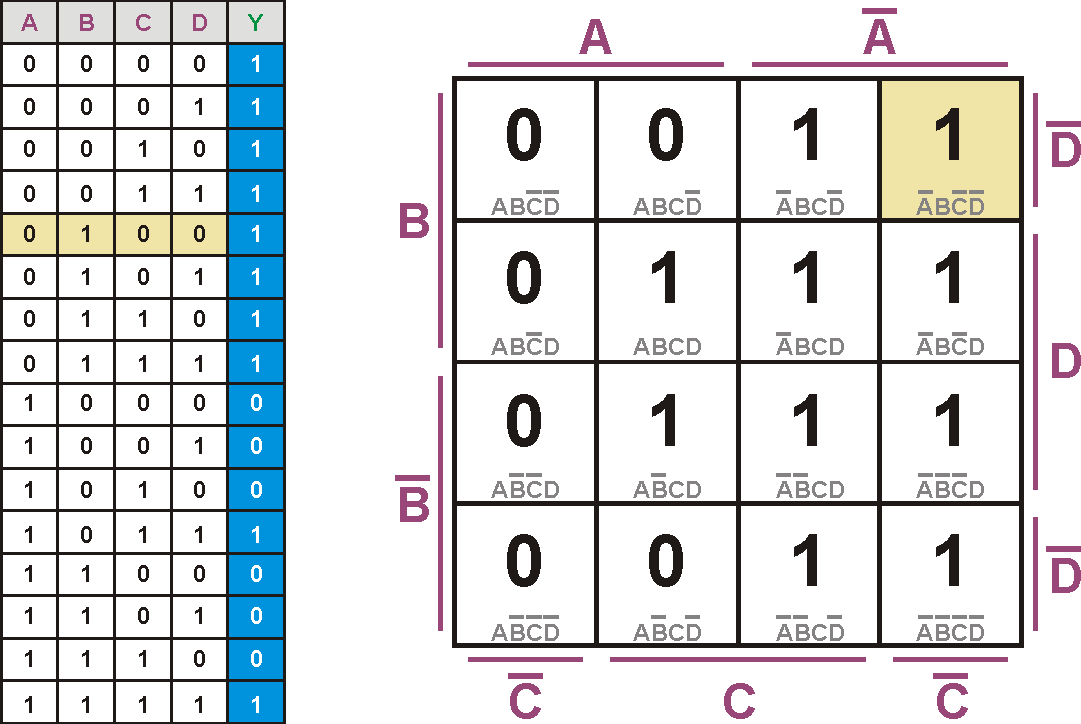
Blockbildung
Ohne Vereinfachung würde die Logikgleichung aus der Tabelle wie folgt lauten:
$$ \scriptsize Y = \overline{ABCD} + \overline{ABC} D + \overline{AB} C \overline{D} + \overline{AB} CD + \overline{A} B \overline{CD} + \overline{A} B \overline{C} D + \overline{A} BC \overline{D} + \overline{A} BCD + A \overline{B} CD + ABCD$$
Alle Kombinationen, bei denen der Ausgang auf 1 geht, sind ODER-verknüpft. Würde man diese Formel schaltungstechnisch umsetzen, bräuchte man 4 Inverter, 10 UND-Gatter mit 4 Eingängen und ein 10-fach ODER.
Um die Gleichung zu vereinfachen, wird versucht, im KV-Diagramm Zellen mit gleichem Inhalt zu Blöcken zusammenzufassen. Je größer die Blöcke, desto einfacher wird das Ergebnis. Dabei müssen aber bestimmte Regeln eingehalten werden.
Die Blöcke müssen immer rechteckig sein und die Größe einer Zweierpotenz haben, also 2, 4, 8, 16, 32, usw. Die Blöcke können auch über den Rand hinaus gehen und mit der gegenüber liegenden Seite verbunden werden, denn man kann sich das KV-Diagramm auch mehrfach nebeneinander vorstellen. Blöcke können sich teilweise überlappen. Das kann sinnvoll sein, wenn dadurch größere Blöcke entstehen.
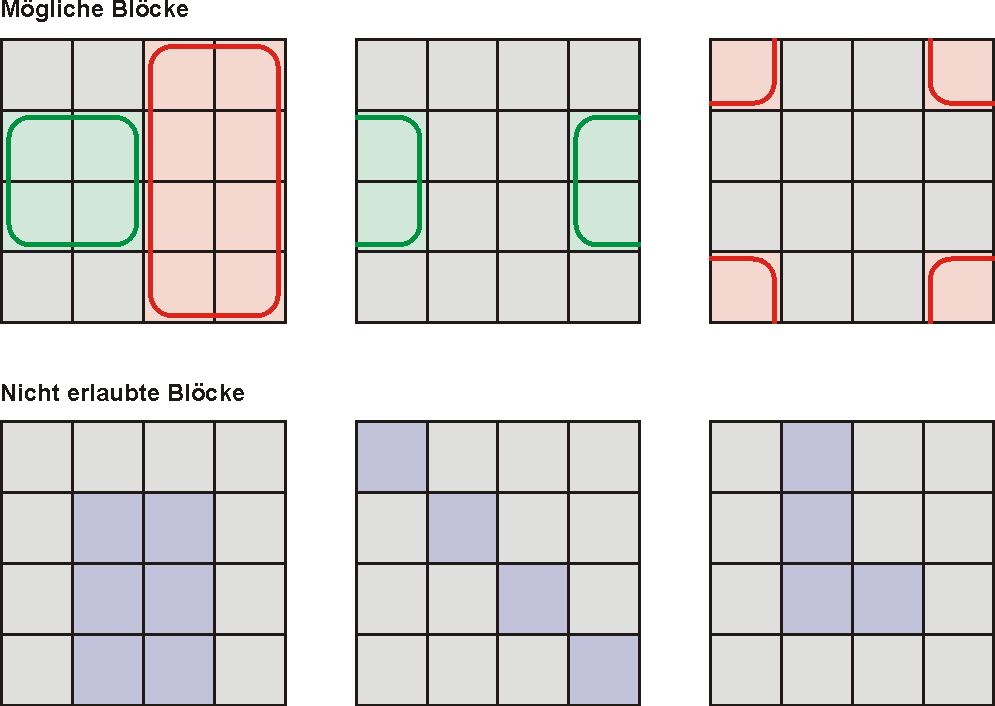
Es gibt zwei verschiedene Ansätze bei der Vereinfachung abhängig davon, ob man die Felder zusammenfasst, die den Wert 1 ergeben oder Felder mit der 0.
Minterm-Methode
- Felder mit dem Inhalt 1 werden zu möglichst großen Blöcken zusammengefasst
- Die Eingangswerte, die von den Blöcken berührt werden, werden UND-verknüpft
- Werte, die sowohl einfach als auch negiert vorkommen, werden gestrichen
- Die Blöcke werden dann miteinander ODER-verknüpft
Die Werte B, C und D kommen doppelt vor und können deshalb entfallen. Für den roten Block bleibt einfach nur $\overline{A}$.
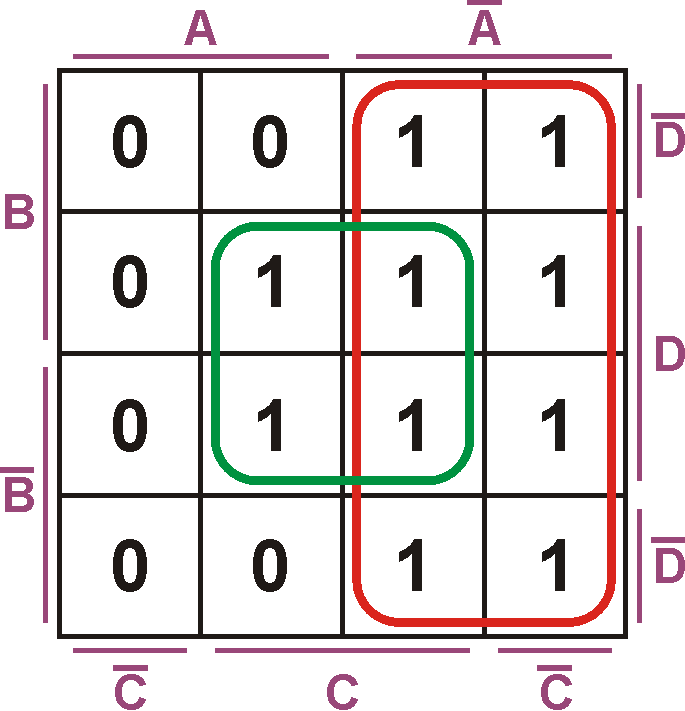
Die zwei Felder links, die nicht vom roten Block erfasst wurden, könnte man zwar zu einem Zweierblock zusammenfassen. Da Blöcke sich überschneiden können, ist hier die bessere Lösung, einen Viererblock zu bilden.
Der grüne Block umfasst jetzt die Werte: $A\overline{A}B\overline{B}CD$.
A und B sind überflüssig. Es bleibt die UND-Verknüpfung $CD$.
Mit den zwei Blöcken sind alle Felder erfasst. Die Ergebnisse der Blöcke werden jetzt nur noch ODER-verknüpft und von der langen Formel am Anfang bleibt nur noch
$$Y = \overline{A} + CD.$$
Der zweite Weg sollte jetzt zum gleichen Ergebnis führen.
Maxterm-Methode
- Felder mit dem Inhalt 0 werden zusammengefasst
- Die Ausdrücke in den Blöcken werden ODER-verknüpft
- Doppelte Werte werden wieder gestrichen
- Die Blöcke werden miteinander UND-verknüpft
- Zusätzlich müssen die einzelnen Werte negiert werden
Nach dem Streichen von B und D bleibt $A + \overline{C}$. Jetzt müssen noch die Werte negiert werden, also ist die Lösung für den roten Block: $\overline{A} + C$.
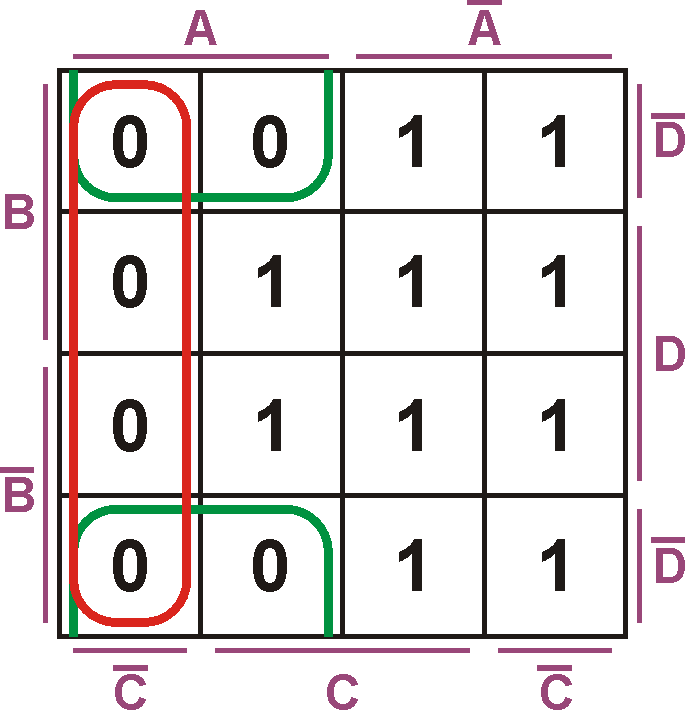
Der grüne Block ergibt: $A + B + \overline{B} + C + \overline{C} + \overline{D}$
Nachdem B und C entfallen, bleibt $A +\overline{D}$ und nach der Negation $\overline{A} + D$. Nach der UND-Verknüpfung beider Blöcke lautet das Ergebnis:
$$Y = (\overline{A} + C) \cdot (\overline{A} + D).$$
Das sieht jetzt erst mal nicht nach dem Ergebnis von vorhin aus. Allerdings lässt sich die Klammer auflösen (siehe Regel 14 auf der vorigen Seite) zu:
$$Y = \overline{A} + CD.$$