Der Arbeitspunkt
Bevor wir zu den Verstärkern kommen müssen wir erst mal den Begriff Arbeitspunkt klären, denn er wird eine wichtige Rolle spielen. Der Arbeitspunkt zeigt den aktuellen Betriebszustand einer Schaltung an. Zu jedem Bauelement gibt es eine Reihe von Kennlinien. Als Beispiel nehmen wir die Strom-Spannungs-Kennlinie eines einfachen ohmschen Widerstandes an. Das ist eine Gerade, beginnend im Nullpunkt des Koordinatensystems. Die Steigung der Geraden hängt vom Wert des Widerstandes ab, in unserem Beispiel 200Ω. Wollen wir wissen, welcher Strom bei einer Spannung von 2V fließt, gehen wir von dem Punkt auf der Spannungsachse senkrecht in Richtung Kennlinie. Am Schnittpunkt legen wir eine waagerechte Gerade zur Stromachse und lesen dort einen Strom von 10mA ab. Der Schnittpunkt auf der Kennlinie ist unser erster Arbeitspunkt.
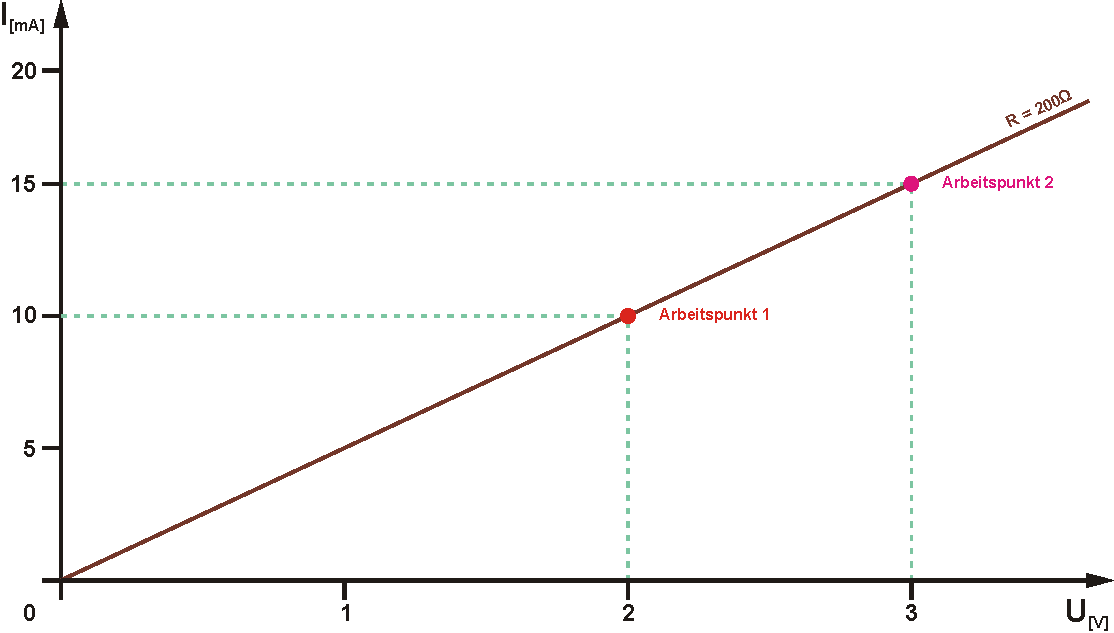
Ändern sich die äußeren Bedingungen, verschiebt sich der Arbeitspunkt auf der Kennlinie. In der Abbildung liegt der Arbeitspunkt 2 zum Beispiel bei 3V und 15mA.
Der Widerstand von aktiven Bauelementen ist leider nicht so konstant wie beim ohmschen Widerstand. Damit bei Verstärkern keine Verzerrungen entstehen, sollte sich der Ruhearbeitspunkt der Schaltung, das heißt der Arbeitspunkt ohne Signal, möglichst in der Mitte eines linearen Bereiches der Kennlinie befinden.
Das Kennlinienfeld des Bipolartransistors
Warum die Einstellung des Ruhearbeitspunktes beim Verstärker so wichtig ist, sehen wir uns an der Eingangskennlinie des Transistors an, die nichts anderes ist als die Strom-Spannungs-Kennlinie der Basis-Emitter-Diode. Damit ein angelegtes Signal nicht verzerrt wird, sollte die Ausgangsgröße, also der Basisstrom, möglichst linear der Eingangsgröße, der Basis-Emitter-Spannung, folgen. Was aus einem Signal wird, sieht man, wenn man es an der Kennlinie spiegelt. Ausgehend vom Ruhezustand bewegt sich der Arbeitspunkt mit der Aussteuerung auf der Kennlinie entlang. Eine verzerrungsfreie Übertragung gibt es nur, wenn die Kennlinie in dem Bereich möglichst eine Gerade ist.
Ein Wechselspannungssignal würde von der Basis-Emitter-Diode normalerweise gleichgerichtet werden. Während der negativen Halbwelle kann kein Strom fließen, aber auch in Durchlassrichtung fließt erst ab der Schwellspannung der Diode überhaupt ein Strom. In der linken Abbildung ist zu sehen, wie der Basisstromverlauf (grün) im Gegensatz zu Eingangssignal (blau) aussieht.
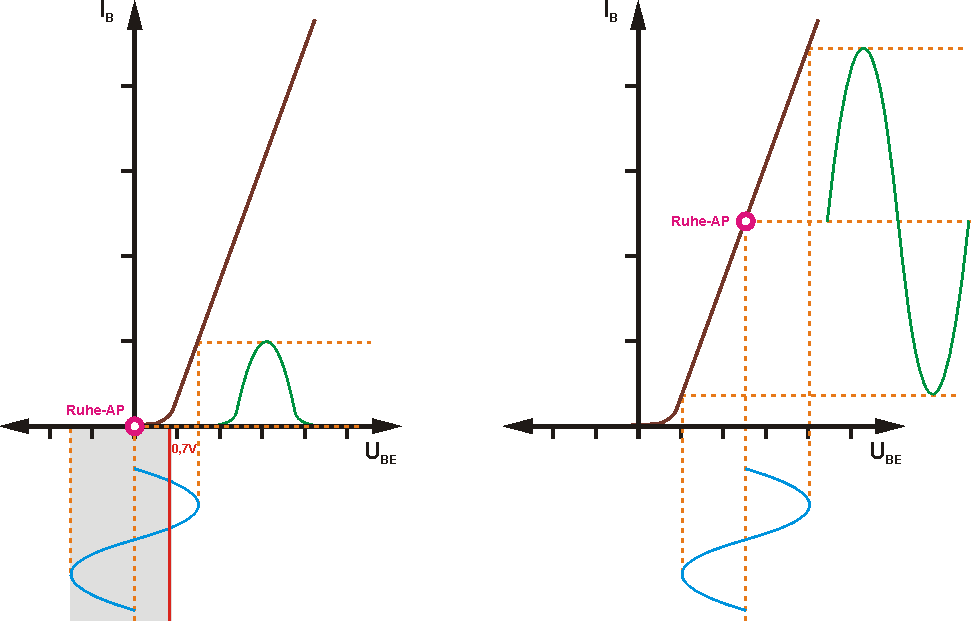
Besser sieht es aus, wenn wir den Ruhearbeitspunkt in einen möglichst linearen Bereich der Kennlinie legen (Abbildung rechts). Jetzt kann der Basisstrom genau dem Eingangssignal folgen. Dazu müssen wir dafür sorgen, dass bereits ohne Eingangssignal ein gewisser Basisstrom fließt.
Auf dem Weg zum Ausgang der Verstärkerstufe durchläuft das Signal mehrere Kennlinien. Die Basis-Emitter-Spannung erzeugt einen Basisstrom. Der Basisstrom steuert den höheren Kollektorstrom entsprechend der Stromverstärkung. Auch der Zusammenhang sollte natürlich möglichst linear sein. Am Ende bildet die Kollektor-Emitter-Strecke einen Spannungsteiler mit dem Arbeitswiderstand. Bei einem rein ohmschen Widerstand ist die Strom-Spannungs-Kennlinie auf jeden Fall eine Gerade. Die untere Abbildung zeigt, wie aus der kleinen Eingangsspannung UBE die Ausgangsspannung UCE wird, über den Umweg der Stromsteuerkennlinie, denn der Bipolartransistor ist stromgesteuert.
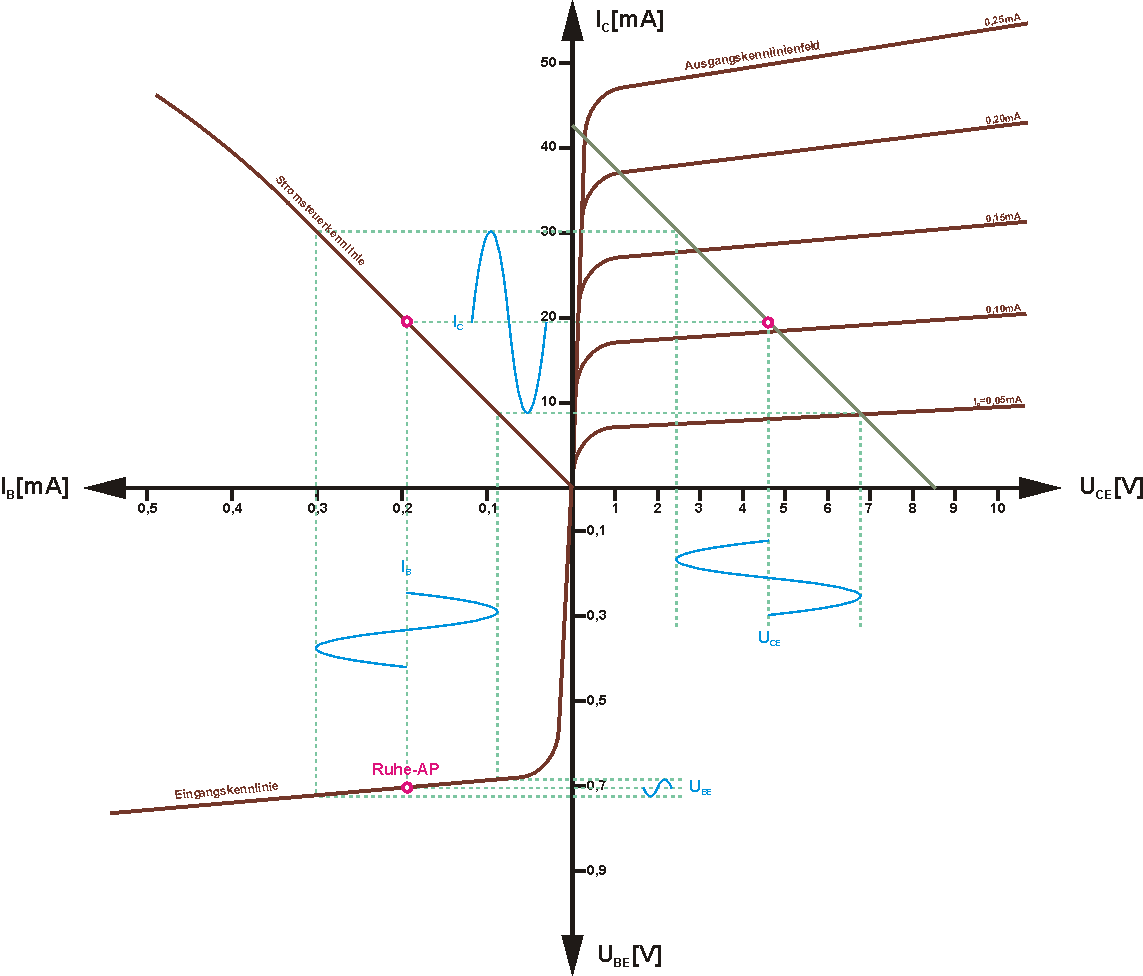
Um eine einfache Transistor Verstärkerstufe zu dimensionieren, sehen wir uns das Ausgangskennlinienfeld etwas genauer an. Bei der Festlegung des Arbeitspunktes dürfen die Grenzwerte des Transistors nicht überschritten werden. Deshalb sollten diese eingezeichnet werden. Das ist die maximal zulässige Kollektor-Emitter-Spannung, der maximale Kollektorstrom und die maximal zulässige Verlustleistung, die am Transistor in Wärme umgewandelt wird. Sie ist das Produkt aus Strom und Spannung am Transistor. Verbindet man alle Punkte, an denen dieses Produkt gleich ist, entsteht eine Hyperbel. Das bedeutet, der rote Bereich ist für den Arbeitspunkt verboten, da mindestens ein Grenzwert überschritten würde.
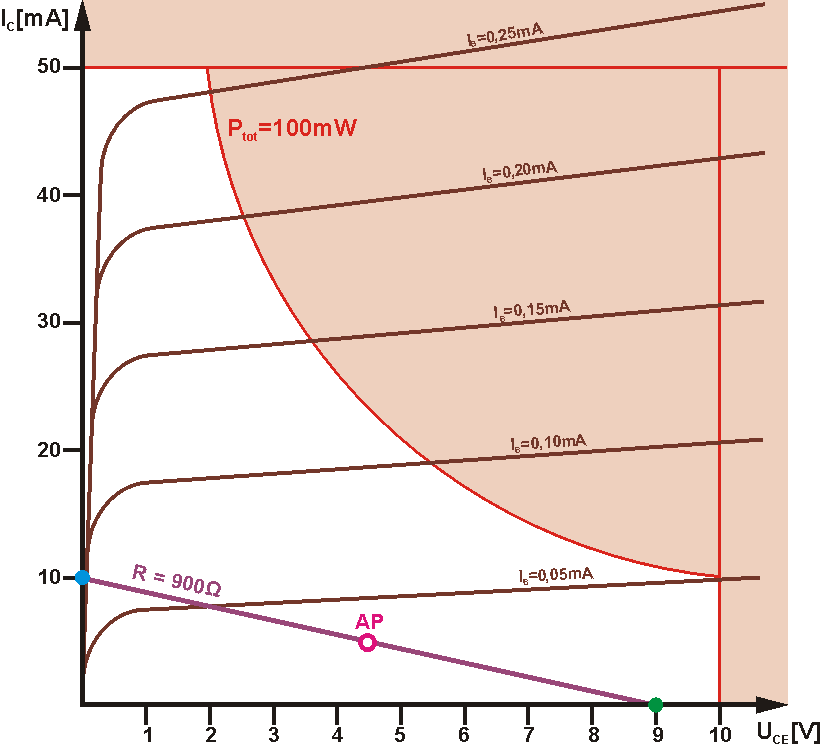
Der Arbeitspunkt bewegt sich entlang einer Geraden, die vom Kollektorwiderstand abhängig ist. Da die Spannung am Transistor entgegengesetzt verläuft wie am Arbeitswiderstand, ist die Arbeitsgerade im Kennlinienfeld eine gedrehte Widerstandsgerade. Um sie einzuzeichnen, benötigt man zwei Punkte und dafür nimmt man die beiden Extremwerte. Bei gesperrtem Transistor ist der Strom 0 und über dem Transistor liegt die volle Betriebsspannung. Im Beispiel wählen wir 9V. Dort ist der Punkt auf der x-Achse (grün). Ist der Transistor voll durchgesteuert, ist die Spannung 0 und der Strom wird nur durch den Kollektorwiderstand bestimmt. Mit dem ohmschen Gesetz kann man den Strom und damit den Schnittpunkt auf der y-Achse ausrechnen (blauer Punkt). Wir nehmen mal 900Ω. Das sind dann 10mA.
Je niedriger der Arbeitswiderstand wird, umso steiler verläuft die Gerade. Dabei muss man darauf achten, dass die Gerade nicht durch den roten Bereich gehen darf.
Transistorstufe mit Bipolartransistor
Für eine maximale mögliche Aussteuerung nach beiden Seiten sollte der Ruhearbeitspunkt in der Mitte liegen. Das entspricht UCE=4,5V und ICA=5mA. Um den Ruhestrom fließen zu lassen, muss der Transistor einen Basisstrom bekommen, der um den Faktor der Stromverstärkung geringer ist. Das wird durch einen Widerstand gegen die Betriebsspannung erreicht.
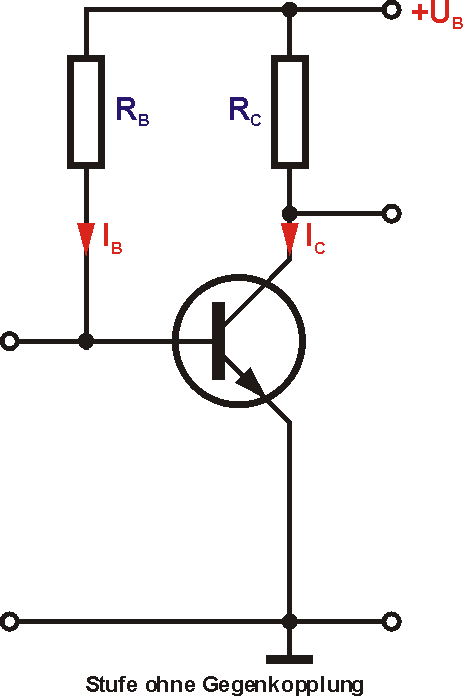
Diese einfache Transistorstufe hat den Nachteil, dass der Arbeitspunkt mit der Eigenerwärmung des Transistors "wegläuft". Durch die bessere Leitfähigkeit steigt der Kollektorstrom mit der Temperatur an. Deshalb muss man Maßnahmen treffen, um den Arbeitspunkt stabil zu halten. Die erste Möglichkeit ist die sogenannte Spannungsgegenkopplung, bei der der Basiswiderstand nicht mit der Betriebsspannung, sondern mit dem Kollektor des Transistors verbunden wird.
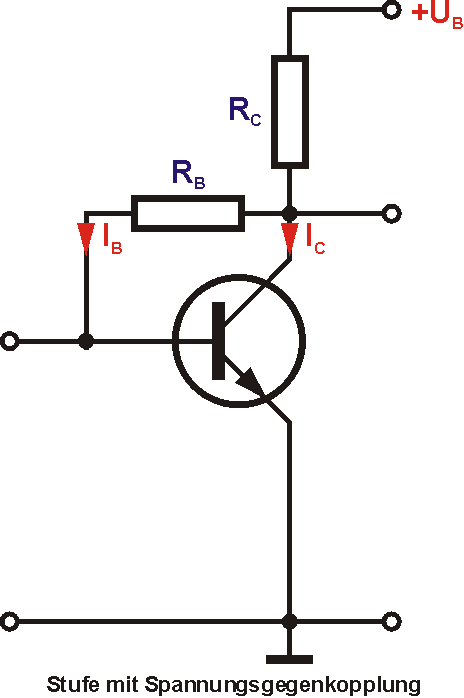
Mit steigendem Kollektorstrom wird der Spannungsabfall an RC größer und damit sinkt die Kollektor-Emitter-Spannung. Somit sinkt auch die Basis-Emitter-Spannung und dadurch auch der Basisstrom. Ein kleinerer Basisstrom lässt den Kollektorstrom wieder sinken und der Arbeitspunkt wird wieder korrigiert. Berechnen wir die Widerstände anhand unseres Zahlenbeispiels.
Durch den Kollektorwiderstand fließt jetzt zusätzlich der Basisstrom. Bei ausreichend hoher Stromverstärkung kann der gegenüber dem Kollektorstrom aber vernachlässigt werden. Der Kollektorwiderstand ist die halbe Betriebsspannung, geteilt durch den Kollektorstrom im Arbeitspunkt.
$$R_C \approx \frac{U_B}{2 \cdot I_{CA}} \approx \frac{4,5V}{5mA} \approx 900Ω$$
Der Ruhebasisstrom im Arbeitspunkt ist der Kollektorstrom, geteilt durch die Stromverstärkung des Transistors. Wir setzen B=200 an.
$$I_B = \frac{I_{CA}}{B} = \frac{5mA}{200} = 25 \mu A$$
Am Basiswiderstand liegt die Kollektorspannung abzüglich der Basis-Emitter-Spannung, was der Flussspannung der Basis-Emitterdiode entspricht.
$$R_B = \frac{(U_{CE}-U_{BE})}{I_B} = \frac{(4,5V-0,7V)}{25 \mu A} = 152kΩ$$
Die zweite Stabilisierungsmöglichkeit ist eine Stromgegenkopplung über einen Emitterwiderstand. Der Basisspannungsteiler soll die Basisspannung möglichst konstant halten. Die Arbeitspunktstabilisierung funktioniert wie folgt.
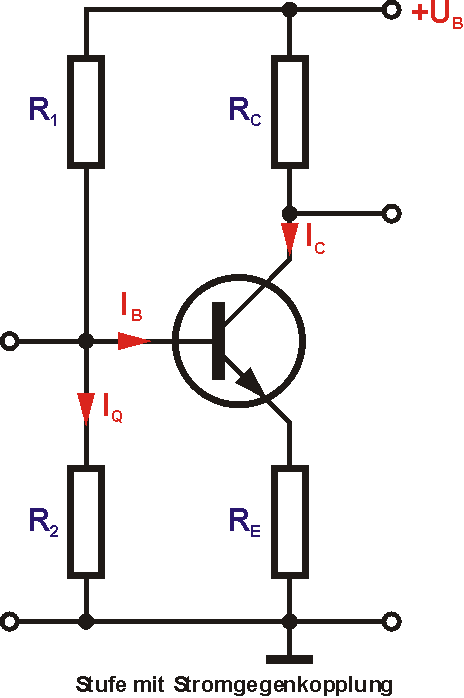
Die Basisspannung ist die Summe aus der Basis-Emitter-Spannung und dem Spannungsabfall über RE. Wenn der Kollektorstrom durch Temperaturerhöhung steigt, wird auch die Spannung über RE größer. Bei konstanter Spannung am Spannungsteiler aus R1 und R2 sinkt dadurch die Basis-Emitter-Spannung. Der Basisstrom sinkt und damit auch wieder der Kollektorstrom.
Die Berechnung der Widerstände richtet sich nach dem Grad der Gegenkopplung. Für eine ausreichende Temperaturstabilität reichen erfahrungsgemäß etwa 0,7V bis 1,0V über dem Emitterwiderstand aus. Wir setzen für unsere Rechnung 0,8V an. Damit liegt die Basisspannung bei Siliziumtransistoren bei 1,5V. Durch den Emitterwiderstand fließt sowohl der Kollektor-, als auch der Basisstrom. Den vernachlässigen wir aber wieder. Damit ergibt sich für den Emitterwiderstand:
$$R_E \approx \frac{U_{RE}}{I_{CA}} \approx \frac{0,8V}{5mA} \approx 160Ω.$$
Durch den Kollektorwiderstand fließen in Ruhe ebenfalls 5mA. Die Spannung über ihm ist die Differenz aus Betriebsspannung minus den Spannungen über dem Transistor und dem Emitterwiderstand. Damit errechnet sich seine Größe zu:
$$R_C = \frac{U_B - U_{CE} - U_{RE}}{I_{CA}} = \frac{9V - 4,5V - 0,8V}{5mA} = 740Ω.$$
Der Spannungsteiler aus R1 und R2 soll die Spannung an der Basis auf 1,5V halten. Über beide Widerstände fließt ein Querstrom IQ von der Betriebsspannung zur Masse. Durch R1 fließt zusätzlich der Basisstrom. Es gibt beliebig viele Kombinationen von R1 und R2, die die Spannung auf 1,5V herunter teilen. Wie geht man also an die Berechnung heran? Im Betrieb überlagert das Eingangssignal die Basisspannung und der Basisstrom schwankt. Die Basisspannung bleibt also nicht ganz konstant, da sich der Spannungsabfall über R1 im Takt des Signals ändert. Um den Einfluss des Basisstroms möglichst gering zu halten, sollte er im Vergleich zum Querstrom möglichst klein sein. Das bedeutet, R1 und R2 sollten möglichst niederohmig sein, damit der Querstrom groß wird. Allerdings wird dadurch die Stromaufnahme der Stufe höher und der Eingangswiderstand sinkt. Man muss einen Kompromiss finden. In der Praxis arbeitet man mit einem Querstrom-Basisstrom-Verhältnis von 5 bis 10. In unserem Fall ist der Basisstrom wieder 25μA. Wir rechnen mit einem 5-mal höheren Querstrom.
$$m = \frac{I_Q}{I_B} = 5...10$$
$$I_Q = 5 \cdot I_B = 5 \cdot 25μA = 125μA$$
Jetzt können wir R2 berechnen.
$$R2 = \frac{U_{R2}}{I_Q} = \frac{1,5V}{125μA} = 12kΩ$$
Bei der Berechnung von R1 müssen wir berücksichtigen, dass durch ihn auch der Basisstrom fließt.
$$R1 = \frac{U_B - U_{R2}}{I_Q + I_B} = \frac{9V - 1,5V}{125μA + 25μA} = 50kΩ$$
Die Gegenkopplung über RE wirkt sich nicht nur auf den Ruhestrom aus. Auch das Wechselspannungssignal wird hier gegengekoppelt. Dadurch sinkt die Verstärkung, allerdings verringern sich auch die nichtlinearen Verzerrungen. Will man die Gegenkopplung für das Signal ausschalten, muss man den Emitterwiderstand mit einem ausreichend hohen Kondensator überbrücken.
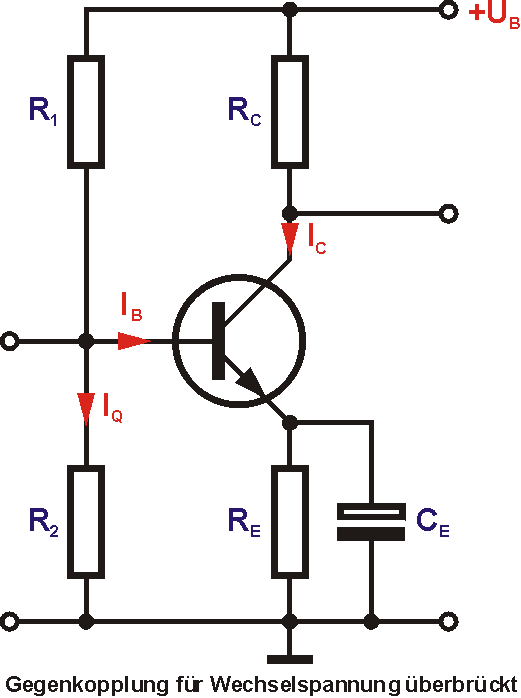
Transistorstufe mit Feldeffekttransistor
Die Berechnung von Transistorstufen mit selbstsperrenden Feldeffekttransistoren ist ähnlich der von Bipolartransistoren. In den Gateanschluss fließt allerdings kein Ruhestrom, sodass der Spannungsteiler am Gate sehr hochohmig ausfallen kann. Der Feldeffekttransistor ist spannungsgesteuert. Deshalb spricht man bei ihm, wie bei der Elektronenröhre, nicht von einer Stromverstärkung, sondern von der Steilheit. Das ist das Verhältnis von Änderung des Drainstroms zur Änderung der Gatespannung in mA je Volt.
$$S = \frac{\Delta I_D}{\Delta U_{GS}}$$
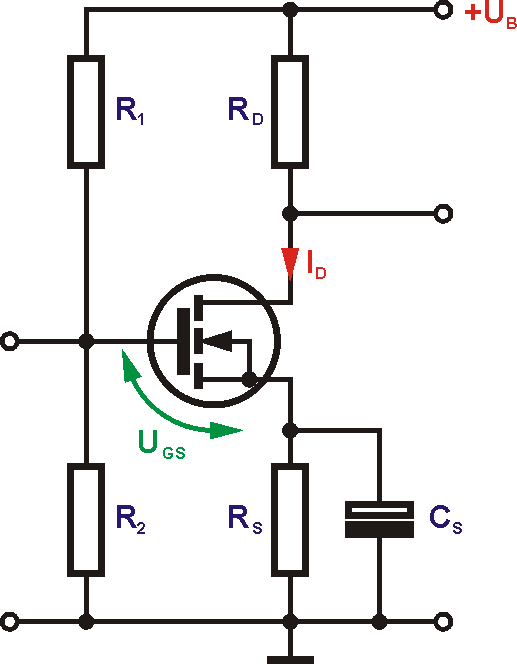
Über R1 und R2 erhält das Gate eine Vorspannung, die so gewählt wird, dass über dem Transistor wieder etwa die halbe Betriebsspannung steht. RS dient wieder der Temperaturstabilisierung und kann durch CS für das Signal überbrückt werden.
Bei selbst leitenden Feldeffekttransistoren, also JFETs oder Verarmungs-MOSFETs, kann die Vorspannung nicht aus der Betriebsspannung gewonnen werden, da sie eine umgekehrte Polarität haben muss. Beim n-Kanal JFET wäre das eine negative Spannung. Man nutzt hier das Prinzip der automatischen Vorspannungserzeugung, das schon von der Elektronenröhre bekannt ist. Das Gate wird über einen hochohmigen Widerstand mit Masse verbunden. Da so gut wie kein Strom durch den Widerstand fließt, hat das Gate annähernd Massepotential.
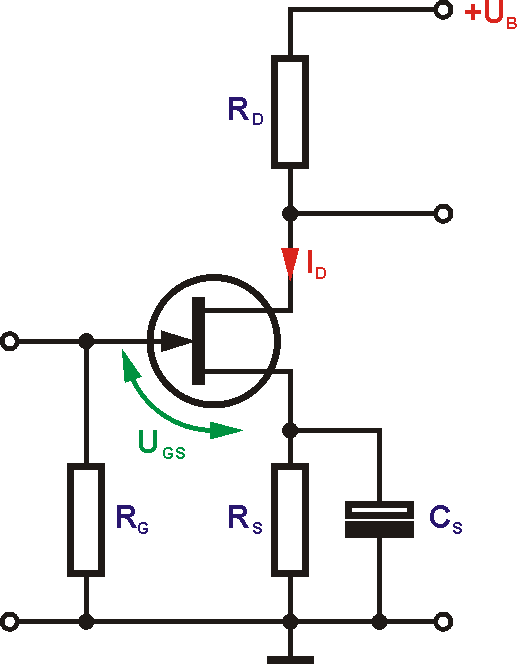
Der Drain-Ruhestrom verursacht über dem Sourcewiderstand einen Spannungsabfall. Dadurch wird das Source-Potential hoch gelegt. Der Sourceanschluss hat gegenüber der Masse eine positivere Spannung. Das bedeutet, das Gate ist jetzt negativer als der Sourceanschluss, was wir ja erreichen wollten. Die Größe des Sourcewiderstandes berechnet sich als Quotient aus der Gatevorspannung und dem Drain-Ruhestrom. $$R_S = \frac{U_{GS}}{I_D}$$