Schaltung und Logikgleichung
In den nächsten beiden Abschnitten geht es darum, Logikschaltungen zu optimieren. Am Anfang steht oft eine Logiktabelle, in der man den gewünschten Zustand des Ausgangs bei den verschiedenen Kombinationen am Eingang auflistet. Daraus lässt sich dann eine Logikgleichung aufstellen. Bevor man das in eine Schaltung mit Logikgattern umsetzt, sollte man die Gleichung so weit es geht kürzen bzw. optimieren, um die Anzahl der Gatter zu minimieren. Nehmen wir an, die Gleichung sieht so aus: $$Y = (\overline{A} + B) \cdot (\overline{AB})$$ Dann ergibt sich daraus die unten stehende Zusammenschaltung von Logikgattern. Der Ausgang Y geht auf 1 bzw. High, wenn die Bedingungen in der Gleichung erfüllt sind. Im oberen Zweig wird zunächst der Pegel der Eingangsleitung A negiert und geht danach mit B auf ein ODER-Gatter. Das entspricht der ersten Klammer in der Gleichung. Im unteren Teil gehen A und B auf ein NAND-Gatter. Beide Werte werden also UND-verknüpft und das Ergebnis invertiert. Das ist die rechte Klammer. Anschließend werden beide Terme UND-verknüpft.
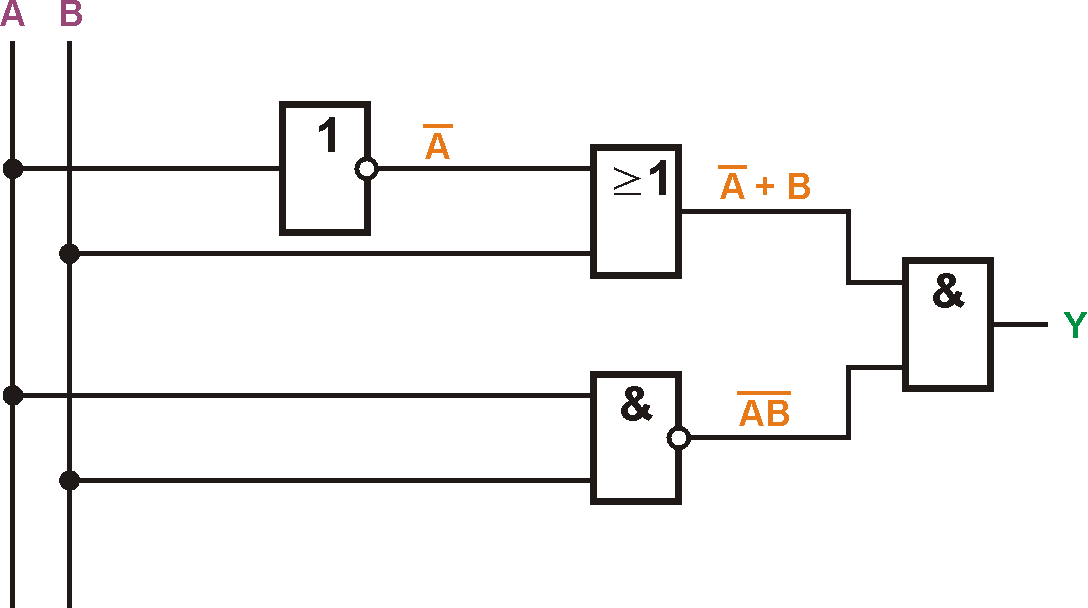
Es kommen 4 verschiedene Gattertypen zum Einsatz. Die Frage ist, lässt sich der Zusammenhang einer Ausgangsgröße mit nur zwei Eingangsgrößen nicht einfacher realisieren? Dazu sehen wir uns an, welche Regeln es zur Vereinfachung einer Logikgleichung gibt.
Viele der Regeln lassen sich aus einfachen Überlegungen herleiten. Eine UND-Verknüpfung mit einer 0 ergibt immer 0, denn so lange ein Eingang auf 0 ist, wird die UND-Bedingung nicht erfüllt (Regel 1). Regel 9 sagt, dass ein Wert zweimal negiert wieder den ursprünglichen Wert ergibt. Auch die Regeln 10 und 11 sind nicht schwer zu verstehen, denn sie besagen, dass man die Eingänge beliebig vertauschen kann.
| 1 | $0 \cdot A = 0$ | Konjunktion mit 0 |
|---|---|---|
| 2 | $1 \cdot A = A$ | Konjunktion mit 1 |
| 3 | $A \cdot A = A$ | Konjunktion mit sich selbst |
| 4 | $A \cdot \overline{A} = 0$ | Konjunktion mit inversem Wert |
| 5 | $0 + A = A$ | Disjunktion mit 0 |
| 6 | $1 + A = 1$ | Disjunktion mit 1 |
| 7 | $A + A = A$ | Disjunktion mit sich selbst |
| 8 | $A + \overline{A} = 1$ | Disjunktion mit inversem Wert |
| 9 | $\overline{\overline{A}} = A$ | Doppelte Negation |
| 10 | $A \cdot B = B \cdot A$ | Kommutativgesetz |
| 11 | $A + B = B + A$ | Kommutativgesetz |
| 12 | $A \cdot B \cdot C = A \cdot (B \cdot C)$ | Assoziativgesetz |
| 13 | $A + B + C = A + (B + C)$ | Assoziativgesetz |
| 14 | $A \cdot (B + C) = (A \cdot B) + (A \cdot C)$ | Distributivgesetz |
| 15 | $A + (B \cdot C) = (A + B) \cdot (A + C)$ | Distributivgesetz |
| 16 | $\overline{(A \cdot B)} = \overline{A} + \overline{B}$ | De morgansche Regel |
| 17 | $\overline{(A + B)} = \overline{A} \cdot \overline{B}$ | De morgansche Regel |
| 18 | $A + (A \cdot B) = A$ | Kürzungsregel |
| 19 | $A \cdot (A + B) = A$ | Kürzungsregel |
| 20 | $A + (\overline{A} \cdot B) = A + B$ | Kürzungsregel |
| 21 | $A \cdot (\overline{A} + B) = A \cdot B$ | Kürzungsregel |
| 22 | $(A \cdot B) + (A \cdot \overline{B}) = A$ | Kürzungsregel |
| 23 | $(A + B) \cdot (A + \overline{B}) = A$ | Kürzungsregel |
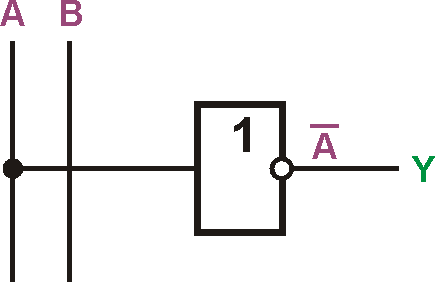
Wenden wir die Regeln geschickt auf das oben stehende Beispiel an. $$Y = (\overline{A} + B) \cdot (\overline{AB})$$ Mit der De morganschen Regel 16 wird daraus $$Y = (\overline{A} + B) \cdot (\overline{A} + \overline{B}).$$ Da jetzt A quer sowohl mit B als auch mit dem inversen Wert von B verknüpft die Bedingung der Gleichung erfüllt, bedeutet das, dass B jeden Wert haben kann und eigentlich keine Rolle spielt. Mit der Regel 23 wird deshalb daraus $$Y = \overline{A}.$$ Es reicht ein einfacher Inverter an Anschluss A. Die anderen drei Gatter sind völlig überflüssig.
Weitere Beispiele könnt ihr in dem oben verlinkten Video sehen.