Mit den Übungsaufgaben kann jeder überprüfen, ob das jeweilige Thema wirklich verstanden wurde. Tut euch selbst einen Gefallen und deckt nicht gleich die Lösung auf. Versucht es erst einmal selbst. Ein paar mathematische Grundkenntnisse, wie das richtige Umstellen von Formeln, setze ich allerdings voraus.
Aufgabe 1:
Eine 12V-Lampe soll über eine Entfernung von 1km mit einer 12V-Batterie betrieben werden. Dazu soll ein zweiadriges Aluminiumkabel verwendet werden, bei dem jeder Leiter einen Durchmesser von 2,25mm hat. Der spezifische Widerstand von Aluminium ist $0,0278 \Omega \frac{mm^2}{m}$. Die Lampe hat einen Widerstand von 40Ω. Lässt sich die Lampe unter diesen Bedingungen vernünftig betreiben?
Lösung 1: ![]()
Unser Stromkreis besteht aus einer Reihenschaltung von 3 Widerständen, die beiden Zuleitungen des Versorgungskabels und unsere Lampe. Wie hoch ist der Spannungsabfall über dem Kabel, bzw. welche Spannung liegt noch an der Lampe an?
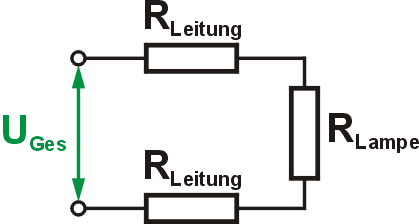
Für die Berechnung benötigen wir zunächst den Widerstand unseres Kabels. Den Leitungsquerschnitt berechnen wir über die Kreisflächenformel aus dem Durchmesser der Leitung. $$R_{Leitung} = ρ \cdot \frac{l}{A} = ρ \cdot \frac{l}{\pi \cdot {(\frac{d}{2})^2}}$$ $$R_{Leitung} = 0,0278 \Omega \frac{mm^2}{m} \cdot \frac{1000m}{3,1416 \cdot (1,125mm)^2} \approx 7 \Omega$$ Die Gesamtspannung verteilt sich wie folgt: $$U_{ges} = U_{Leitung} + U_{Lampe} + U_{Leitung}$$ damit ist $$U_{Lampe} = U_{ges} - 2 \cdot U_{Leitung} = U_{ges} - 2 \cdot I \cdot R_{Leitung}$$ Bei einer Reihenschaltung ist der Strom durch alle Elemente gleich. Wir können ihn nach dem Ohmschen Gesetz als Quotient aus der Gesamtspannung und dem Gesamtwiderstand berechnen. $$U_{Lampe} = U_{ges} - 2 \cdot \frac{U_{ges}}{R_{ges}} \cdot R_{Leitung}$$ $$U_{Lampe} = 12V - 2 \cdot \frac{12V}{54 \Omega} \cdot 7 \Omega \approx 8,889V$$ Über der Lampe liegt nur noch knapp 3/4 der Nennspannung an. Sie wird zwar leuchten, aber mit erheblich geringerer Lichtstärke. Das Beispiel zeigt, dass man den Leitungswiderstand selbst bei gut leitenden Materialien und relativ großen Querschnitten nicht unterschätzen darf.
Aufgabe 2:
Wie ändern sich die Verhältnisse, wenn wir an unseren Stromkreis aus Aufgabe 1 eine 120V-Spannungsquelle anschließen und die 12V-Lampe durch eine 120V-Lampe mit der gleichen Nennleistung ersetzen?
Lösung 2: ![]()
Zuerst berechnen wir die Nennleistung der 12V-Lampe aus Aufgabe 1, das heißt die Leistung, wenn sie mit ihrer Nennspannung 12V betrieben wird: $$P = U \cdot I = U \cdot \frac{U}{R_{Lampe}} = \frac{(12V)^2}{40 \Omega} = 3,6W$$ Für unsere Formel aus Aufgabe 1 benötigen wir jetzt noch den Widerstand der 120V-Lampe: $$R_{Lampe} = \frac{U_{Lampe}}{I} = \frac{U_{Lampe}}{\frac{P}{U_{Lampe}}} = \frac{(120V)^2}{3,6W} = 4k \Omega$$ Mit der Formel aus der ersten Aufgabe können wir jetzt wieder berechnen, welche Spannung bei der Lampe ankommt. Die Leitungswiderstände sind mit jeweils 7 Ω unverändert: $$U_{Lampe} = U_{ges} - 2 \cdot \frac{U_{ges}}{R_{ges}} \cdot R_{Leitung}$$ $$U_{Lampe} = 120V - 2 \cdot \frac{120V}{4014 \Omega} \cdot 7 \Omega \approx 119,58V$$ Bei der 12V-Variante ging uns etwa 1/4 der Spannung durch die Zuleitung verloren. Bei der 120V-Variante ist die Spannung an der Lampe nur unwesentlich geringer, als an der Spannungsquelle. Mit höherer Spannung kann man also Energie verlustfreier übertragen, weshalb der Transport über große Entfernungen auf Hochspannungstrassen erfolgt.
Aufgabe 3:
Welche Versorgungsspannung müssen wir an den Stromkreis in Aufgabe 1 anlegen, damit an der Lampe die vollen 12V zur Verfügung stehen?
Lösung 3: ![]()
$$U_{ges} = 2 \cdot U_{Leitung} + U_{Lampe}$$ Die Lampenspannung ist gegeben mit 12V. Den Spannungsabfall über der Leitung müssen wir uns wieder aus dem Ohmschen Gesetz herleiten: $$U_{ges} = 2 \cdot I \cdot R_{Leitung} + U_{Lampe}$$ Der Strom ist wieder im gesamten Stromkreis gleich. Den Strom durch die Lampe können wir aus bekannten Größen (Lampenspannung und -widerstand) bestimmen: $$U_{ges} = 2 \cdot \frac{U_{Lampe}}{R_{Lampe}} \cdot R_{Leitung} + U_{Lampe}$$ $$U_{ges} = 2 \cdot \frac{12V}{40 \Omega} \cdot 7 \Omega + 12V = 16,2V$$ Wer jetzt dachte, man müsse einfach nur den in Aufgabe 1 errechneten Spannungsverlust zu den 12V dazugeben, der irrt. Der Grund dafür ist, dass der Strom in Aufgabe 3 höher ist als in Aufgabe 1, wodurch über den Leitungswiderständen ein höherer Spannungsabfall entsteht.
Aufgabe 4:
Aus einem Drehspulinstrument möchten wir uns durch entsprechende Vor- und Nebenwiderstände ein einfaches Multimeter bauen (siehe Abbildung). Es soll je 4 Spannungsmessbereiche (0,5V, 10V, 100V, 1000V) und 4 Strommessbereiche (500μA, 10mA, 100mA, 1A) haben. Unser Instrument hat einen Innenwiderstand von 4kΩ und zeigt bei einem Strom von 100μA Vollausschlag an.
Wie groß müssen die Widerstände R1 bis R8 sein?
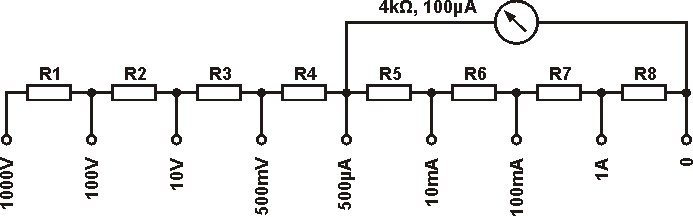
Betrachten wir zuerst den kleinsten Strommessbereich 500μA, bei dem die Einspeisung am Knotenpunkt zwischen R4 und R5 erfolgt. Unser Instrument schlägt schon bei 100μA voll aus. Der Rest des Stromes (400μA) wird deshalb über die Widerstände R5 bis R8 am Instrument vorbeigeführt. In unseren Berechnungen bezeichnen wir den Strom durch das Instrument mit IInstr und den Strom durch die Nebenwiderstände mit IN, die dazugehörigen Widerstände entsprechend.
Die Ströme in beiden Zweigen verhalten sich umgekehrt proportional zu den Widerständen. Wir können den erforderlichen Nebenwiderstand wie folgt berechnen:
$$\frac{R_N}{R_{Instr}} = \frac{I_{Instr}}{I_N}$$
$$R_{N(500μA)} = R_{Instr} \cdot \frac{I_{Instr}}{I_N} = 4k \Omega \cdot \frac{100μA}{400μA} = 1k \Omega.$$
Die Widerstände R5 bis R8 müssen also zusammen einen Wert von 1k Ω haben.
Nehmen wir uns jetzt den nächsten Messbereich 10mA vor. Im Instrumentenzweig liegt jetzt R5 in Reihe zum Messwerk und R6 bis R8 sind die Nebenwiderstände, durch die jetzt 9,9mA am Instrument vorbeifließen müssen. In unserer oberen Formel ist RInstr jetzt die Summe aus R5 und dem Innenwiderstand des Messwerkes. Dummerweise kennen wir R5 aber noch nicht, das heißt wir müssen ihn anderweitig herleiten. Wir brauchen also eine weitere bekannte Größe. Wenn wir uns die Strommessbereiche ansehen, dann fließt der Strom immer auf unterschiedlichen Wegen durch R5 bis R8 und das Instrument. Die Summe aller Widerstände bleibt immer gleich und wir kennen sie aus der ersten Berechnung: RG = 4kΩ + 1kΩ = 5 kΩ. Achtung, das ist nicht der Widerstand, den unser Multimeter nach außen hin zeigt!
Wir können RInstr durch die Differenz aus RG und RN ersetzen und dann die Formel neu umstellen.
$$R_N = (R_G - R_N) \cdot \frac{I_{Instr}}{I_N} = R_G \cdot \frac{I_{Instr}}{I_N} - R_N \cdot \frac{I_{Instr}}{I_N}$$
$$R_N + R_N \cdot \frac{I_{Instr}}{I_N} = R_N \cdot \frac{I_N+I_{Instr}}{I_N} = R_G \cdot \frac{I_{Instr}}{I_N}$$
$$R_{N(10mA)} = R_G \cdot \frac{I_{Instr}}{I_{Instr}+I_N}= 5000 \Omega \cdot \frac{0,1mA}{10mA} = 50 \Omega.$$
R6 bis R8 ergeben zusammen 50Ω. Damit können wir jetzt den Wert von R5 berechnen:
$$R5 = R_G - R_{Messwerk} - R_{N(10mA)} = 5000 \Omega - 4000 \Omega - 50 \Omega = 950 \Omega$$
Mit unserer Formel können wir als Nächstes die Summe aus R7 und R8 berechnen, die im 100mA-Bereich als Nebenwiderstand fungieren:
$$R_{N(100mA)} = R_G \cdot \frac{I_{Instr}}{I_{Instr}+I_N}= 5000 \Omega \cdot \frac{0,1mA}{100mA} = 5 \Omega$$
$$R6 = R_G - R_{Messwerk} - R5 - R_{N(100mA)} = 5000 \Omega - 4000 \Omega - 950 \Omega - 5 \Omega = 45 \Omega$$
Im letzten Messbereich besteht der Nebenwiderstand nur noch aus R8
$$R_{N(1A)} = R8 = R_G \cdot \frac{I_{Instr}}{I_{Instr}+I_N}= 5000 \Omega \cdot \frac{0,1mA}{1000mA} = 0,5 \Omega.$$
Damit ergibt sich R7 quasi als Rest:
$$R7 = R_{N(100mA)} - R8 = 5 \Omega - 0,5 \Omega = 4,5 \Omega.$$
Die Strommessbereiche hätten wir somit erledigt. Fehlen uns noch die Vorwiderstände, wenn wir unser Multimeter als Spannungsmesser verwenden wollen. Dazu sehen wir den bisher betrachteten Teil zwischen Nulleiter und Knoten R4/R5 als Einheit an. Wir wissen, dass wir dort bei einem Strom von 500μA einen Vollausschlag bekommen. Der Gesamtwiderstand besteht aus der Parallelschaltung des Instrumentes und den Nebenwiderständen.
$$R_{Ges} = \frac {R_{Messwerk} \cdot R_{N(500μA)}}{R_{Messwerk} + R_{N(500μA)}} = \frac {4k \Omega \cdot 1k \Omega}{5k \Omega} = 0,8k \Omega$$
Bei Vollausschlag liegt an der Einheit eine Spannung von
$$U = R_{Ges} \cdot I = 800 \Omega \cdot 0,5A = 0,4V$$
an. Unser kleinster Spannungsmessbereich soll bis 0,5V gehen. Die Differenz 0,1V muss am Widerstand R4 abfallen.
$$R4 = \frac {0,1V}{0,5 \cdot 10^{-3} A} = 200 \Omega$$
Beim 10V-Bereich müssen weitere 9,5V an R3 anliegen
$$R3 = \frac {9,5V}{0,5 \cdot 10^{-3} A} = 19 \cdot 10^{3} \Omega = 19k \Omega$$
R2 und R1 berechnen wir analog
$$R2 = \frac {90V}{0,5 \cdot 10^{-3} A} = 180 \cdot 10^{3} \Omega = 180k \Omega$$
$$R1 = \frac {900V}{0,5 \cdot 10^{-3} A} = 1,8 \cdot 10^{6} \Omega = 1,8M \Omega.$$
Damit ist unser Schaltbild komplett.
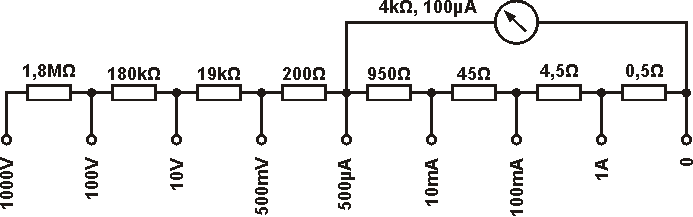
Aufgabe 5:
Wir benutzen unser Messinstrument aus Aufgabe 4 als Voltmeter an einer Reihenschaltung von 2 Widerständen mit je 10kΩ. Die angelegte Gesamtspannung beträgt 10V und wir benutzen auch den 10V-Messbereich an unserem Messgerät. Welche Spannungsanzeige bekommen wir über dem Widerstand R2?
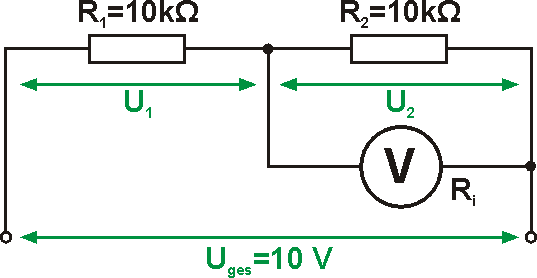
Hat jemand spontan 5V gesagt? Natürlich liegt bei 2 gleichen Widerständen in Reihe über jedem Widerstand die halbe Spannung an und das würde ein ideales Messgerät auch anzeigen. Unser Messgerät hat aber einen Innenwiderstand, der jetzt parallel zu R2 liegt. Damit hat die Parallelschaltung von R2 und Ri einen kleineren Wert als R1 und so wird auch die Spannung, die über dem Messgerät liegt, jetzt kleiner. Berechnen wir zunächst einmal den Innenwiderstand Ri.
4 Widerstände in Reihe (R5-R8) liegen parallel zum Messinstrument und die ganze Anordnung dann noch in Reihe mit R3 und R4.
$$R_{i} = R3 + R4 + \frac {(R5+R6+R7+R8) \cdot R_{instr}}{(R5+R6+R7+R8) + R_{instr}} = 19k \Omega + 0,2k \Omega + \frac {1k \Omega \cdot 4k \Omega}{1k \Omega + 4k \Omega} = 20k \Omega$$
Die Parallelschaltung von Ri und R2 ergibt
$$R_i \parallel R_2 = \frac {R_i \cdot R_2}{R_i + R_2} = \frac {20k \Omega \cdot 10k \Omega}{20k \Omega + 10k \Omega} = 6,666\overline6kΩ$$
Wir können jetzt den Gesamtstrom berechnen und dann die Spannung über R1, da durch R1 auch der Gesamtstrom fließt:
$$I_{ges} = \frac {U_{ges}}{R_{ges}} = \frac {U_{ges}}{R_2 + (R_i \parallel R_2)} = \frac {10V}{10k \Omega + 6,666\overline6k \Omega} = 0,6mA$$
$$U_1 = R_1 \cdot I_{ges} = 10k \Omega \cdot 0,6mA = 6V$$
Das bedeutet für die Spannung am Instrument:
$$U_{R_i \parallel R_2} = U{ges} - U_1 = 10V - 6V = 4V$$
Wir messen also eine erheblich geringere Spannung an R2. Der Messfehler beträgt immerhin 20%! Das Beispiel soll zeigen, wie durch ein Messinstrument die realen Werte verfälscht werden können, besonders wenn der Innenwiderstand des Messgerätes sich in der gleichen Größenordnung bewegt, wie die Widerstände in der Schaltung. Machen wir die Rechnung mit zwei 100Ω-Widerständen, messen wir an R2 eine Spannung von 4,9875V und die Messabweichung ist nur 0,25%.
Aufgabe 6:
In unserer sechsten Aufgabe wollen wir einen Transformator für unser 230V Wechselstromnetz berechnen. Auf der Sekundärseite soll er uns bereitstellen: 120V, 250mA und 5V, 2A. Was benötigen wir, um uns den Trafo selbst zu wickeln?
Lösung 6: ![]()
Als Erstes berechnen wir die zu übertragene Leistung.
$$P_{sekundär} = 120V \cdot 0,25A + 5V \cdot 2A = 30VA + 10VA = 40 VA$$
$$P_{primär} = 1,18 \cdot P_{sekudär} = 1,18 \cdot 40VA = 47,2VA$$
Aus der Tabelle entnehmen wir, dass als Trafokern sowohl der M 74 als auch der EI 85a infrage kommen. Beide sind für eine Leistung von 50VA ausgelegt. Der Primärstrom beträgt
$$I_{primär} = \frac {P_{primär}}{U_{primär}} = \frac {47,2VA}{230V} \approx0,205A$$
Wir entscheiden uns für den M 74-Kern. Mit den Werten aus der Tabelle errechnen wir die Windungszahlen:
$$w_{primär} = 5,4 \frac{Wdg.}{V} \cdot 230V = 1242Wdg.$$
$$w_{sekundär1} = 6 \frac{Wdg.}{V} \cdot 120V = 720Wdg.$$
$$w_{sekundär2} = 6 \frac{Wdg.}{V} \cdot 5V = 30Wdg.$$
Für die Primärspule brauchen wir einen 0,32mm CuL-Draht, für die 5V-Wicklung einen Draht mit 1,0mm Durchmesser und für die 120V Wicklung einen 0,36mm CuL-Draht.
Überprüfen wir noch, ob genug Platz für unsere Wicklungen zur Verfügung steht. Dazu berechnen wir, welchen Querschnitt unsere Wicklungen in Anspruch nehmen.
$$A_{Primärspule} = \frac {1242Wdg.}{690\frac{Wdg.}{cm^2}} = 1,8 cm^2$$
$$A_{Sekundärspule1} = \frac {720Wdg.}{540\frac{Wdg.}{cm^2}} \approx 1,333 cm^2$$
$$A_{Sekundärspule2} = \frac {30Wdg.}{83\frac{Wdg.}{cm^2}} \approx 0,36 cm^2$$
Das macht einen benötigten Wicklungsquerschnitt von etwa 3,5 cm2. Aus der ausnutzbaren Fensterhöhe und -breite des M 74-Kerns errechnen wir den nutzbaren Fensterquerschnitt mit 5,28 cm2. Wir haben also noch etwas Reserve, um zusätzliche Isolationen zwischen den Wicklungen unterzubringen. Als Letztes berechnen wir noch die benötigten Drahtlängen. Wir wickeln zuerst unsere Primärspule und dann darüber die Sekundärwicklungen. Wir rechnen großzügig bei der Primärspule mit der mittleren und bei den Sekundärspulen mit der äußeren Wicklungslänge.
$$l_{primär} = 16,5 \frac{cm}{Wdg.} \cdot 1242Wdg. \approx 205m$$
$$l_{sekundär1} = 19,8 \frac{cm}{Wdg.} \cdot 720Wdg. \approx 143m$$
$$l_{sekundär2} = 19,8 \frac{cm}{Wdg.} \cdot 30Wdg. \approx 6m$$
Aufgabe 7:
Wir wollen ein Netzteil mit einer Gleichrichterröhre UY82 aufbauen. Laut Datenblatt darf der Ladekondensator maximal 100μF groß sein. Die Leerlaufspannung am Ladekondensator beträgt 250V. Das Netzteil soll einen Maximalstrom von 100mA liefern. Bei Volllast soll die Brummspannung höchstens 0,1% betragen und die Ausgangsspannung maximal um 10V absinken.
Berechne die Werte der notwendigen RC-Siebkette. Wie groß muss die Induktivität bei einer LC-Siebung sein, wenn wir auch für den Siebkondensator nur einen 100μF Elko zur Verfügung haben?
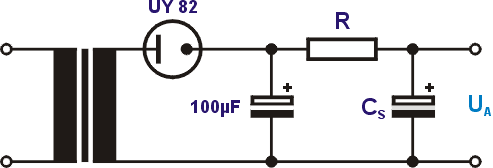
Da über dem Siebwiderstand maximal 10V Spannung abfallen darf, berechnen wir zunächst dessen Maximalwert und die Verlustleistung, die er aushalten muss: $$R = \frac {U}{I} = \frac {10V}{0,1A} = 100 \Omega$$ $$P = U \cdot I = 10V \cdot 0,1A = 1W$$ Mit den Formeln aus dem Kapitel Schaltungstechnik berechnen wir jetzt die Brummspannung vor der Siebkette am Ladekondensator: $$\Delta U_1 = 5 \cdot 10^{-3} s \cdot \frac{I}{C_L} = 5 \cdot 10^{-3} s \cdot \frac{0,1A}{100 \cdot 10^{-6} F} = 5V$$ Laut Aufgabenstellung darf die Brummspannung am Ausgang maximal 0,25V sein. Bei einem Siebwiderstand von 100Ω errechnet sich der Wert des Siebkondensators zu $$C_S = 3,2 \cdot 10^{-3} s \cdot \frac{\Delta U_1}{\Delta U_2 \cdot R} = 3,2 \cdot 10^{-3} s \cdot \frac{5V}{0,25V \cdot 100 \Omega} = 640 \mu F$$ Durch Umstellung der Faustformel für die LC-Siebkette können wir die Induktivität bei einem 100μF großen Siebkondensator berechnen: $$L = 10^{-5} s^2 \cdot \frac{\Delta U_1}{\Delta U_2 \cdot C_S} = 10^{-5} s^2 \cdot \frac{5V}{0,25V \cdot 100 \cdot 10^{-6}F} = 2H$$ Die Spule muß natürlich so dimensioniert sein, dass der ohmsche Widerstand der Drahtwicklung 100Ω nicht überschreitet.
Aufgabe 8:
Die 12V-Spannungsversorgung für eine Schaltung soll mit einer Z-Diode stabilisiert werden. Die Stromaufnahme der Schaltung schwankt zwischen 5mA und 10mA. Die Eingangsspannung darf sich zwischen +10% und -20% ändern. Als Z-Dioden stehen zur Verfügung eine SZX21/12 mit einer maximalen Verlustleistung von 250mW und eine SZ600/12 mit Ptot=0,9W (ohne zusätzliche Kühlung).
Wie groß muss die Eingangsspannung und der Vorwiderstand bei beiden Varianten sein?
Der Vorwiderstand muss sowohl der Formel für den maximalen RV als auch der für den minimalen RV genügen. Wir setzen deshalb die beiden Formel gleich und stellen sie um. $$\frac{U_{E min} - U_Z}{I_{L max} + I_{Z min}} = \frac{U_{E max} - U_Z}{I_{L min} + I_{Z max}}$$ $$\frac{U_{E min} - U_Z}{U_{E max} - U_Z} = \frac{I_{L max} + I_{Z min}}{I_{L min} + I_{Z max}} = K$$ Den rechten Ausdruck ersetzen wir mit der Variablen K, damit das weitere Umstellen der Formel übersichtlicher wird. Damit wir die Gleichung nach UE umstellen können, ersetzen wir UEmin und UEmax durch UE multipliziert mit einem Abweichungssfaktor q. q+ ist die Abweichung nach oben und q- nach unten. In unserem Fall mit +10% Abweichung nach oben ist q+=1,1 und bei -20% ist q-=0,8. $$\frac{U_E \cdot q_- - U_Z}{U_E \cdot q_+ - U_Z} = K$$ $$U_E \cdot q_- - U_Z = K(U_E \cdot q_+ - U_Z) = K \cdot U_E \cdot q_+ - K \cdot U_Z$$ $$U_E \cdot q_- - K \cdot U_E \cdot q_+ = U_Z - K \cdot U_Z = U_Z (1 - K)$$ $$U_E (q_- - K \cdot q_+) = U_Z (1 - K)$$ $$U_E = U_Z \cdot \frac{1 - K}{q_- - K \cdot q_+}$$ Berechnen wir zunächt K und dann UE für die SZX21/12. Der maximale zulässige Z-Strom beträgt 0,25W / 12V ≈ 20 mA, der minimale Strom 2 mA. $$K = \frac{I_{L max} + I_{Z min}}{I_{L min} + I_{Z max}} = \frac{10mA + 2mA}{5mA + 20mA} = 0,48$$ $$U_E = 12V \cdot \frac{1 - 0,48}{0,8 - 0,48 \cdot 1,1} = 12V \cdot 1,398 \approx 23V$$ Berechnen wir jetzt den Vorwiderstand. $$R_{V max} = \frac{U_{E min} - U_Z}{I_{L max} + I_{Z min}} = \frac{20,7V - 12V}{10mA + 2mA} = 725 \Omega$$ $$R_{V min} = \frac{U_{E max} - U_Z}{I_{L min} + I_{Z max}} = \frac{25,3V - 12V}{5mA + 20mA} = 532 \Omega$$ Wir wählen einen Widerstand mit 620Ω. Im ungünstigsten Fall (maximale Eingangsspannung und maximaler Z-Strom) ist die Verlustleistung am Vorwiderstand $$P = \frac {(U_{E max} - U_Z)^2}{R_V} = \frac{(13,3V)^2}{620 \Omega} = 0,28W.$$ Wir entscheiden uns für einen Typ mit 0,5W. Berechnen wir jetzt die Schaltung mit der SZ600/12. Der maximale Strom durch die Z-Diode beträgt 0,9W / 12V = 75 mA, der minimale Strom 7,5 mA. $$K = \frac{I_{L max} + I_{Z min}}{I_{L min} + I_{Z max}} = \frac{10mA + 7,5mA}{5mA + 75mA} ≈ 0,22$$ $$U_E = 12V \cdot \frac{1 - 0,22}{0,8 - 0,22 \cdot 1,1} = 12V \cdot 1,398 \approx 16,8V$$ $$R_{V max} = \frac{U_{E min} - U_Z}{I_{L max} + I_{Z min}} = \frac{15,1V - 12V}{10mA + 7,5mA} = 177 \Omega$$ $$R_{V min} = \frac{U_{E max} - U_Z}{I_{L min} + I_{Z max}} = \frac{18,5V - 12V}{5mA + 75mA} = 81 \Omega$$ Wir entscheiden uns für einen Widerstand von 130Ω, 0,5W, denn. $$P = \frac{(6,5V)^2}{130 \Omega} = 0,325W.$$ Bei der Variante mit der kleineren Z-Diode fließt insgesamt ein geringerer Strom, den der Trafo zur Verfügung stellen muss. Allerdings ist eine höhere Eingangsspannung nötig. Mit der stärkeren Z-Diode muss der Spannungsunterschied zwischen Eingang und Ausgang nicht mehr so groß sein.
Aufgabe 9:
Zur Lösung der Aufgabe werden Kenntnisse aus dem Kapitel Schaltungstechnik - Stromversorgung vorausgesetzt. Für eine Schaltung wollen wir über einen einfachen Längsregler eine stabilisierte Spannung von 5V / 1A zur Verfügung stellen. Die Eingangsspannung beträgt 8V. In unserer Bastelkiste finden wir folgende Bauelemente, die dafür infrage kämen:
Eine Z-Diode SZX21/5,6 mit Ptot=250mW und UZ ≈ 5,6V;
Diverse russische Ge-Kleinleistungstransistoren МП20 mit PVmax = 150mW, ICmax = 300mA mit Stromverstärkungen β um die 60;
Ein Ge-Leistungstransistor GD160B, PVmax = 5,3W, ICmax = 3A mit β = 40.
Dimensioniere die Schaltung und überprüfe die Einhaltung der Grenzwerte aller Bauelemente.
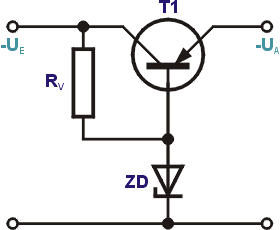
Bei einem Laststrom von 1A kommt für den Regler nur der Leistungstransistor infrage. Wir berechnen den erforderlichen Basisstrom und IZ. $$I_B = \frac{I_L}{\beta} = \frac{1A}{40} = 25mA$$ $$I_Z = 5 \cdot I_B = 125mA$$ Der maximal zulässige Strom bei unserer Z-Diode beträgt aber nur $$I_{Zmax} = \frac{P_{tot}}{U_Z} = \frac{0,25W}{5,6V} \approx 40mA.$$ So funktioniert das nicht. Wir brauchen entweder eine wesentlich leistungsfähigere Z-Diode, oder einen Transistor mit höherer Stromverstärkung. Vielleicht können wir einen der anderen Transistoren mit dem Leistungstransistor zur Darlingtonschaltung zusammenschalten. $$\beta_{ges} = \beta_{T1} \cdot \beta_{T2} = 40 \cdot 60 = 2400$$ $$I_B = \frac{I_L}{\beta} = \frac{1A}{2400} = 0,42mA$$ $$I_{Zmin} = 5 \cdot I_B = 2,1mA$$ Das sieht schon besser aus. Allerdings unterschreitet das noch den mimimalen Z-Strom, der bei 4 mA liegt. Wir legen einfach einen Z-Strom von 10 mA fest und können jetzt den Vorwiderstand berechnen. $$R_V = \frac{U_E - U_Z}{I_Z + I_B} = \frac{8V - 5,6V}{10mA + 0,42mA} \approx 230 \Omega$$ $$P_{R_V} = (U_E - U_Z) \cdot (I_Z + I_B) = (8V - 5,6V) \cdot (10mA + 0,42mA) = 0,024W$$ Überprüfen wir noch, ob die Grenzwerte der anderen Bauelemente eingehalten werden. Der МП20 muss den Basisstrom des GD160 von 25mA bereitstellen. ICmax liegt mit 300mA weit darüber. Die Verlustleistung am GD160 beträgt $$P_{T1} = (U_E - U_A) \cdot I_L = (8V - 5V) \cdot 1A = 3W$$ Das hält unser Transistor aus, er muß aber zur Wärmeabfuhr auf ein Kühlblech geschraubt werden. Wie sieht es am zweiten Transistor aus? Am Kollektor liegt die Eingangsspannung, am Emitter die Ausgangsspannung zuzüglich der Basis-Emitter-Schwellspannung des GD160. $$P_{T2} = (U_E - (U_A + U_{BE_{T1}})) \cdot I_{B_{T1}} = (8V - (5V + 0,3V)) \cdot 25mA = 67,5mW$$ Mit einer maximalen Verlustleistung von 150mW hält das unser МП20 auch aus.
Aufgabe 10:
Für einen Längsregeltransistor in einem Netzteil soll ein Kühlkörper berechnet werden. Die maximal auftretende Spannung über dem Transistor beträgt 6 V. Es soll ein Strom von maximal 1 A entnommen werden. Das Netzteil soll bis zu einer Umgebungstemperatur von 40°C arbeiten. Für die isolierte Montage des Halbleiters rechnen wir mit einem Übergangswiderstand Gehäuse-Kühlkörper von 0,5 K/W. Dem Datenblatt des Transistors entnehmen wir die maximale Sperrschichttemperatur von 150°C und den inneren Wärmewiderstand RthJG = 10 K/W.
Wie groß darf der Wärmewiderstand des Kühlkörpers RthKU maximal sein? Welche Fläche muss ein Aluminiumblech mindestens haben, um ausreichend Kühlung zu bieten?
Am Transistor entsteht eine maximale Verlustleistung von 6V · 1A = 6W.
$$R_{thKU} \leq \frac{T_J - T_U}{P_V} - (R_{thJG} + R_{thGK})$$
$$R_{thKU} \leq \frac{150°C - 40°C}{6W} - (10 \frac{K}{W} + 0,5 \frac{K}{W})$$
$$R_{thKU} \leq 7,833 \frac{K}{W}.$$
Aus dem Diagramm im Anhang lesen wir die Fläche für ein Aluminiumkühlblech von mindestens 110 cm² ab.
In der Praxis sollte immer eine ausreichende Sicherheit mit eingeplant werden. Eine niedrigere Sperrschichttemperatur erhöht die Lebensdauer des Transistors erheblich.