Schaltungstechnik - Stromversorgung

Im Abschnitt Schaltungstechnik geht es um die Berechnung von Schaltungsteilen. Dort wo es möglich ist, werden wir mit Faustformeln für den Praktiker rechnen. Nicht immer ist es nötig, einen Wert mit 5 Stellen hinter dem Komma zu berechnen. Bauelemente haben ohnehin Toleranzen und werden für unsere Schaltungen großzügig bemessen. Das heißt, wir reizen die Grenzwerte unserer Bauelemente nicht aus.

Aus Wechselspannung wird Gleichspannung

In einem klassischen Netzteil wird aus der Netzwechselspannung von 230V über einen Transformator eine Wechselspannung passender Höhe gewonnen. Außerdem erfolgt so eine galvanische Trennung der Schaltung vom Netz. Passende Transformatoren kann man entweder kaufen, aus alten Geräten ausschlachten, bei einer professionellen Trafowickelei herstellen lassen oder, wenn man es sich zutraut, selbst wickeln. Dabei ist Vorsicht beim Umgang mit der Netzspannung angesagt. Die Primärwicklung muss sehr gut von den Sekundärwicklungen isoliert werden. Wie man die Daten für den Trafo ermittelt, kann man nochmals hier und hier nachlesen. Wie wird jetzt daraus eine passende Gleichspannung für unsere Schaltungen?

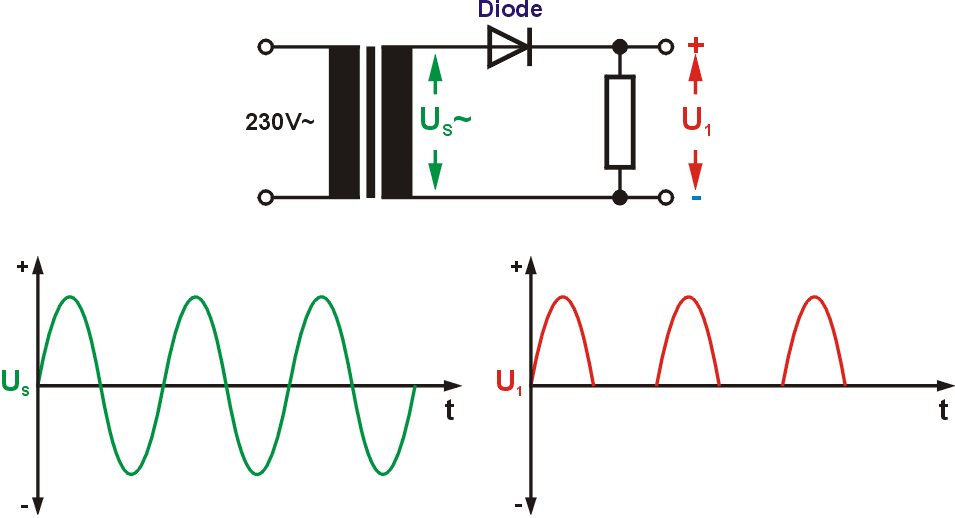
Gleichrichtung

Eine Diode (Röhre oder Halbleiter) lässt den Strom nur noch in eine Richtung fließen und schneidet eine Halbwelle der Wechselspannung ab (siehe Abbildung). Bei dieser Einweggleichrichtung entsteht eine sehr unruhige, pulsierende Gleichspannung, die so noch ungeeignet ist für unsere Zwecke. Nachteilig ist auch, dass von der Eingangsspannung die Hälfte der Energie verschenkt wird.

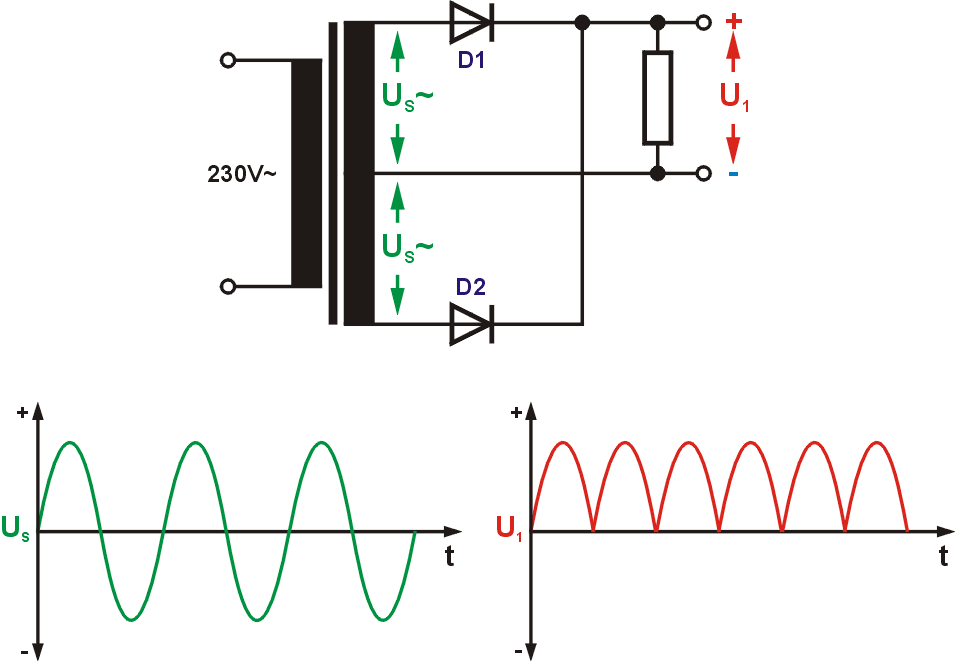
Günstiger wäre es, die negative Halbwelle auch irgendwie zu nutzen. Es gibt zwei Möglichkeiten, eine Zweiweggleichrichtung zu erreichen. Für Variante 1 wird eine zweite sekundäre Trafowicklung benötigt, die entgegengesetzt gepolt ist. Von dort wird über eine zweite Diode die andere Halbwelle zugeführt. So werden die großen Lücken im Spannungsverlauf ausgefüllt.

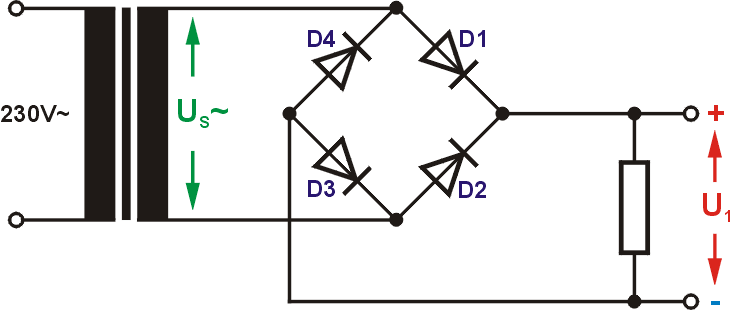
Gegen die erste Variante spricht der erhöhte Aufwand am Transformator. Für uns macht diese Schaltung nur Sinn, wenn ein passender Trafo bereits vorhanden ist. Eine Zweiweggleichrichtung ist aber auch mit nur einer Trafowicklung möglich, es werden dafür allerdings vier Gleichrichterdioden benötigt. Diese Schaltung wird Graetz-Schaltung genannt, nach dem deutschen Physiker Leo Graetz. Während der positiven Halbwelle fließt der Strom über Diode 1 zum Lastwiderstand und durch Diode 3 zurück zum Trafo. Bei der anderen Halbwelle fließt der Strom über D2 und D4.

Glätten und Sieben

Um eine brauchbare Spannung zu erhalten, müssen wir die holprige Gleichspannung glätten. Ein Kondensator hinter dem Gleichrichter kann die großen Spannungsschwankungen ausgleichen. Während der Spannungsspitzen lädt er sich auf und kann in den "Pausen" seine Energie an den Lastwiderstand abgeben. Es bleibt aber eine gewisse Restwelligkeit der Spannung übrig. Man nennt sie auch "Brummspannung", da sie sich in Niederfrequenzschaltungen als störender Brummton bemerkbar macht. Die verbleibende Spannungsschwankung ΔU₁ hängt von der Größe des Ladekondensators und der entnommenen Stromstärke ab. Außerdem ist die Brummspannung bei der Zweiweggleichrichtung geringer, weil der Kondensator öfter nachgeladen wird und die "Lücken", die er überbrücken muss, kleiner sind. Je größer die Kapazität des Kondensators ist, umso glatter wird unsere Spannung. Man benutzt deshalb dafür meist große Elektrolytkondensatoren. Die Größe ist aber auch nach oben begrenzt, da sonst der Ladestrom beim Einschalten zu groß für den Gleichrichter wird. Bei Röhrengleichrichtern findet man in den Datenblättern die Angabe der maximalen Kapazität des Ladekondensators.

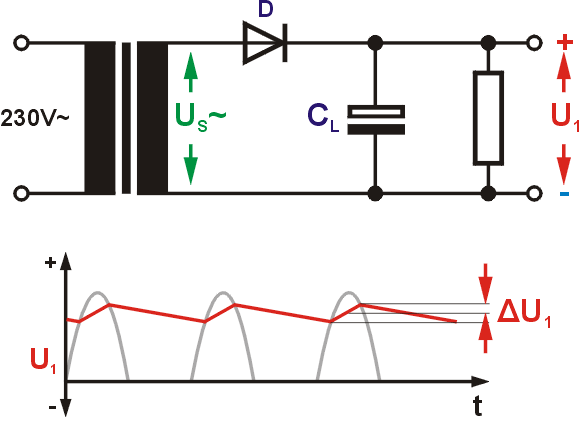
Einweggleichrichtung: $\Delta U_1 = 5 \cdot 10^{-3} s \cdot \frac{I}{C_L}$
Zweiweggleichrichtung: $\Delta U_1 = 2 \cdot 10^{-3} s \cdot \frac{I}{C_L}$

Die verbleibende Welligkeit ist für die Praxis immer noch zu hoch und muss weiter geglättet werden. Deshalb folgt dem Ladekondensator ein weiteres Siebglied aus Kondensator und vorgeschalteter Spule (LC-Siebung) oder vorgeschaltetem Widerstand (RC-Siebung). Bei richtiger Dimensionierung wird die verbleibende Restwelligkeit ΔU₂ verschwindend gering. Für eine LC-Siebung spricht der geringe ohmsche Widerstand der Spule und die bessere Siebwirkung. Nachteilig ist der große Platzbedarf und das Gewicht. Bei der RC-Siebung ist die Ausgangsspannung stärker lastabhängig, da am Widerstand in Abhängigkeit vom entnommenen Strom ein Spannungsabfall entsteht und es wird mehr Wärme produziert.

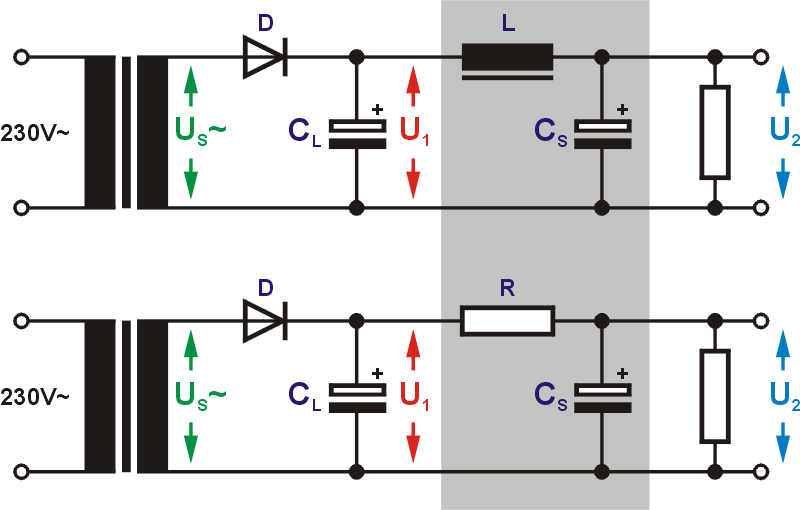
LC-Siebung: $\Delta U_2 = 10^{-5} s^2 \cdot \frac{\Delta U_1}{L \cdot C_S}$
RC-Siebung: $\Delta U_2 = 3,2 \cdot 10^{-3} s \cdot \frac{\Delta U_1}{R \cdot C_S}$

Für die Dimensionierung der Bauelemente sind aber noch andere Dinge entscheidend, die Anfänger oft nicht beachten. Durch die Diode fließt neben dem am Ausgang entnommenen Strom auch ständig ein Ladestrom für den Ladekondensator. Um die Diode nicht zu überlasten, entnehmen wir am Ausgang des Netzteils nicht mehr als das 0,6-fache des maximal zulässigen Durchlassstroms der Diode. Anders gesagt, die Diode muss für einen Strom ausgelegt sein, der um ⅔ größer ist, als der maximale Ausgangsstrom. Am Siebwiderstand wird unter Umständen eine nicht geringe Leistung in Wärme umgesetzt. Der Widerstand muss für diese Leistung dimensioniert sein. Die Kondensatoren laden sich im Leerlauf mit dem Spitzenwert der pulsierenden Spannung auf und müssen dafür ausgelegt sein. Der Spitzenwert ist um den Faktor $\sqrt {2}$ größer als der auf dem Trafo angegebene Effektivwert! Bei der Auswahl des Gleichrichters ist nicht nur der maximal zulässige Strom, sondern auch die maximal zulässige Sperrspannung zu beachten. Dabei wird leicht übersehen, dass die am Gleichrichter maximal auftretende Spannung den doppelten Wert der Spitzenspannung hat! Während der Sperrphase liegt an der Trafoseite der Diode der negative Spitzenwert der Wechselspannung und am anderen Ende ein Kondensator, der mit der positiven Spitzenspannung aufgeladen ist. Der Gleichrichter muss also die doppelte Spannungsfestigkeit der Kondensatoren haben, ausgenommen bei der Greatzschaltung, weil hier immer zwei Dioden in Reihe geschaltet sind und sich die Spannung auf die Dioden verteilt.

Stabile Spannung

Unsere geglättete Spannung ist leider nicht sehr stabil, denn sie schwankt mit der Höhe des entnommenen Stromes. Auch Schwankungen der Eingangsspannung werden an den Ausgang weitergegeben. Eine einfache Möglichkeit der Stabilisierung ist die Verwendung einer passenden Z-Diode. Die Ausgangsspannung entspricht der Z-Spannung (Durchbruchspannung) der in Sperrrichtung gepolten Diode.

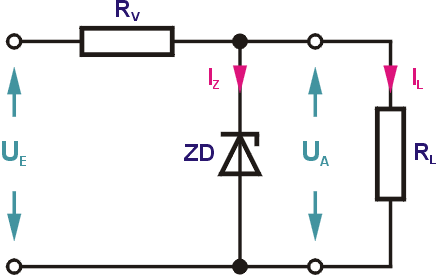
Damit die stabilisierende Wirkung einsetzen kann, muss die Eingangsspannung höher sein, als die Z-Spannung. Durch die Z-Diode fließt ein Strom, der durch einen Vorwiderstand R_V begrenzt wird, damit die Diode keinen Schaden nimmt. Über R_V fällt die Spannungsdifferenz zwischen Ein- und Ausgangsspannung ab. Der Strom verteilt sich auf die Z-Diode und den angeschlossenen Lastwiderstand R_L. Im Leerlauf (Lastwiderstand = ∞) fließt der gesamte Strom über die Diode, die dabei nicht überlastet werden darf. Unter Last wird der Strom durch die Z-Diode geringer. Dass sich dabei auch die Z-Spannung minimal ändert, vernachlässigen wir für unsere Berechnungen. Damit die stabilisierende Wirkung erhalten bleibt, darf der Strom durch die Diode einen minimalen Wert nicht unterschreiten. Wenn der Minimalstrom aus dem Datenblatt nicht zu ermitteln ist, setzt man dafür 10% des Maximalstroms an. Den Maximalwert berechnen wir aus der maximal zulässigen Verlustleistung der Diode P_tot. $$I_{Z max} = \frac{P_{tot}}{U_Z}$$ Für die Berechnung des Vorwiderstandes betrachten wir die zwei möglichen Extremfälle. Bei der minimalen Eingangsspannung und maximalem Laststrom darf I_{Z min} nicht unterschritten werden. Daraus errechnen wir den Maximalwert des Vorwiderstandes: $$R_V \leq \frac{U_{E min} - U_Z}{I_{L max} + I_{Z min}}$$ Bei maximaler Eingangsspannung und minimalem Laststrom darf der maximale Strom durch die Z-Diode nicht überschritten werden und der Vorwiderstand den folgenden Wert nicht unterschreiten: $$R_V \geq \frac{U_{E max} - U_Z}{I_{L min} + I_{Z max}}$$ Nicht zu vergessen ist natürlich die Verlustleistung am Widerstand zu berechnen $P = (U_{E max} - U_Z) \cdot (I_Z + I_L)$. Diese einfache Stabilisierung eignet sich eher für Schaltungen mit relativ geringem Ausgangsstrom und kleinen Lastschwankungen. Eine Beispielrechnung findet sich im Aufgabenteil.

Längsregler

Für höhere Ausgangsströme und Lastschwankungen hilft ein Verstärker im Regelkreis. Dazu verwenden wir einen Transistor in Reihe zum Laststromkreis. Die Referenzspannung liefert wieder eine Z-Diode, die jetzt aber nicht mehr so stark belastet wird. Der Vorwiderstand R_V begrenzt zum einen den Strom durch die Z-Diode und sorgt außerdem dafür, dass ein Basisstrom am Transistor fließt. Über der Basis-Emitter-Diode liegt in Durchlassrichtung die relativ konstante Schwellspannung (0,7V bei Silizium, 0,3V bei Germanium). Die Ausgangsspannung ist darum um die Schwellspannung geringer als die Z-Spannung, das heißt die Z-Spannung muss um diesen Betrag größer sein, als die Ausgangsspannung. Der Transistor ist ein regelbarer Widerstand, über dem die Spannungsdifferenz von Eingangs- und Ausgangsspannung abfällt. Wenn bei größerer Last die Ausgangsspannung sinkt, erhöht sich die Basis-Emitter-Spannung, es fließt ein größerer Basisstrom, der Transistor steuert weiter auf und sein Widerstand sinkt. Dadurch steigt die Spannung wieder auf den ursprünglichen Wert.

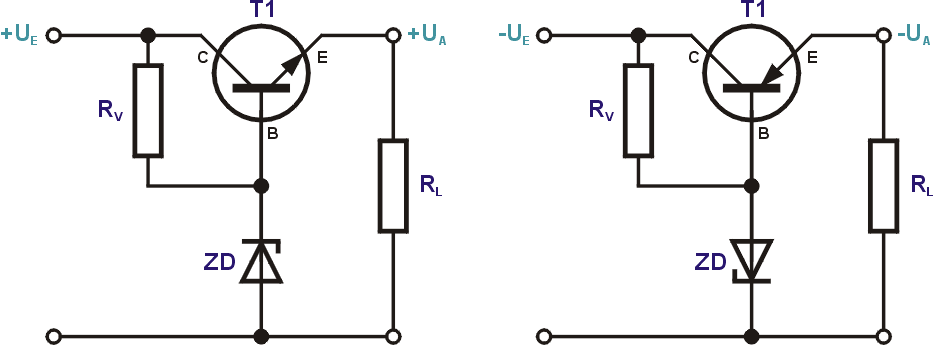
Um die Schaltung zu berechnen, brauchen wir den Stromverstärkungsfaktor β des Transistors. Der Basisstrom ist um diesen Faktor geringer als der Ausgangsstrom. $$I_B = \frac{I_L}{\beta}$$ Um eine gute Stabilisierung zu erreichen und den Einfluss des Basisstroms gering zu halten, sollte der Strom durch die Z-Diode etwa den 5-fachen Wert des Basisstroms haben. $$I_Z = 5 \cdot I_B$$ Durch den Widerstand R_V fließt sowohl I_Z als auch I_B. Mit dem ohmschen Gesetz lässt sich R_V berechnen. $$R_V = \frac{U_E - U_Z}{I_Z + I_B}$$ Wir müssen jetzt noch die Verlustleistungen an R_V, der Z-Diode und dem Transistor berechnen. $$P_{R_V} = (U_E - U_Z) \cdot (I_Z + I_B)$$ $$P_Z = U_Z \cdot I_Z$$ $$P_T = (U_E - U_A) \cdot I_L$$ Darlingtonschaltung
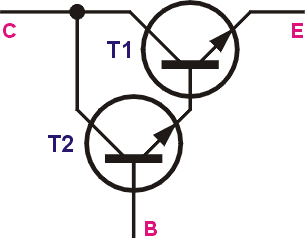
Für den Regeltransistor werden oft Leistungstransistoren benötigt, die allerdings eine relativ geringe Stromverstärkung haben. Um die Stromverstärkung zu erhöhen, kann man zwei Transistoren hintereinander schalten. Die Stromverstärkungen beider Transistoren multiplizieren sich β_ges ≈ β₁ · β₂. Die Verlustleistung am vorgeschalteten Transistor ist in etwa um den Faktor der Stromverstärkung des Leistungstransistors geringer. Da jetzt zwei Basis-Emitter-Dioden in Reihe geschaltet sind, muss die Z-Spannung um weitere 0,7V (bzw. 0,3V) größer sein, als die Ausgangsspannung.

Der Nachteil der bisherigen Schaltungen ist, dass die Ausgangsspannung von der Toleranz der Z-Spannung abhängig ist. Die unten stehende Schaltung bietet die Möglichkeit über einen weiteren Transistor die Sollspannung über den Spannungsteiler R1 und R2 einzustellen. Die Widerstände lassen sich durch einen regelbaren Widerstand ersetzen, mit dem Schleifer an der Basis von T2. Die Referenzspannung liefert wieder eine Z-Diode, die am Emitter von T2 liegt. R_V ist der Vorwiderstand für die Z-Diode. An der Basis von T2 liegt über den Spannungsteiler R1,R2 ein Teil der Ausgangsspannung. U_BE von T2 wird bestimmt von der Ausgangsspannung und der Z-Spannung. Der Kollektorwiderstand R_C von T2 liefert gleichzeitig den Basisstrom für T1.

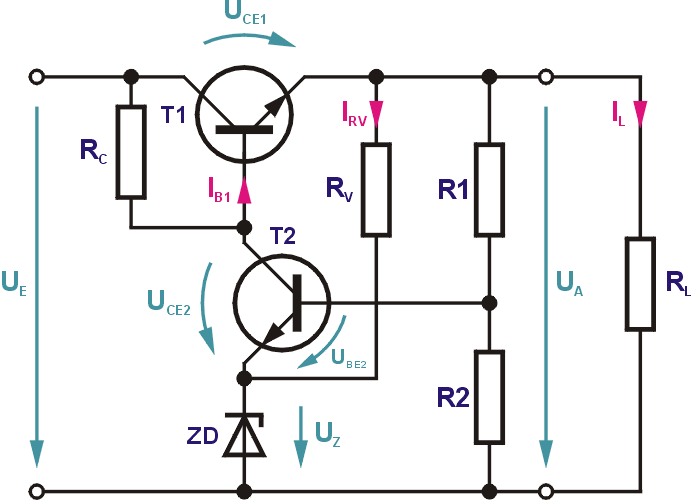
Wie funktioniert das Zusammenspiel? Steigt beispielsweise die Eingangsspannung an, erhöht sich auch U_A. Dadurch steigen auch U_BE2 und I_C2. Der Spannungsabfall über R_C wird größer und damit auch die Spannung zwischen Emitter und Kollektor von T1. Dadurch sinkt die Ausgangsspannung wieder auf den Ausgangswert.
Über das Verhältnis von R1 und R2 kann der Arbeitspunkt von T1 und damit die Höhe der stabilisierten Ausgangsspannung eingestellt werden. Bei der Dimensionierung ist darauf zu achten, dass die Grenzwerte der Bauelemente nicht überschritten werden, wie maximale Verlustleistung, maximale Durchlassströme und Sperrspannungen. Die Ströme müssen größer sein, als die Restströme der Transistoren. Da U_Z und U_A stabilisierte Spannungen sind, kann man die Kollektor-Emitter-Spannung von T2 als konstant ansehen. Es gelten folgende Gleichungen: $$U_A = U_{CE2} + U_Z - U_{BE1}$$ $$U_{CE1} = R_C(I_{C2} + I_{B1}) + U_{BE1}$$ $$\Rightarrow R_C = \frac{U_{CE1} - U_{BE1}}{I_{C2} + I_{B1}}$$ Für die Berechnung von R_C gehen wir von 2 verschiedenen Arbeitspunkten aus.
Fall A: Minimale Eingangsspannung und maximaler Laststrom. $$R_C = \frac{U_{CE1min} - U_{BE1max}}{I_{C2min} + I_{B1max}}$$ Fall B: Maximale Eingangsspannung und minimaler Laststrom. $$R_C = \frac{U_{CE1max} - U_{BE1min}}{I_{C2max} + I_{B1min}}$$ Es gibt zwei Herangehensweisen zur Berechnung von R_C.

Variante 1:

• I_C2min sehr viel größer wählen, als I_B1max
• R_C aus Formel A berechnen.
• I_C2max aus Formel B bestimmen
• Kontrolle, ob I_C2max den Grenzwert nicht überschreitet

Variante 2:

• I_C2max möglichst groß wählen, ohne den Grenzwert zu überschreiten.
• R_C aus U_CE1max = U_Emax - U_A berechnen.
• I_C2min aus Gleichung A bestimmen
• Kontrolle, ob I_C2min viel größer ist als I_B1max

Elektronische Sicherung
Ein zu hoher Laststrom oder gar ein Kurzschluss am Ausgang bedeutet meist das Ende des Stelltransistors. Einfache Schmelzsicherungen sind zu langsam, um den Stromkreis rechtzeitig zu unterbrechen. Darum ist es sinnvoll, das Netzteil mit einer elektronischen Sicherung zu versehen. Die Abbildung zeigt die erweiterte Schaltung.

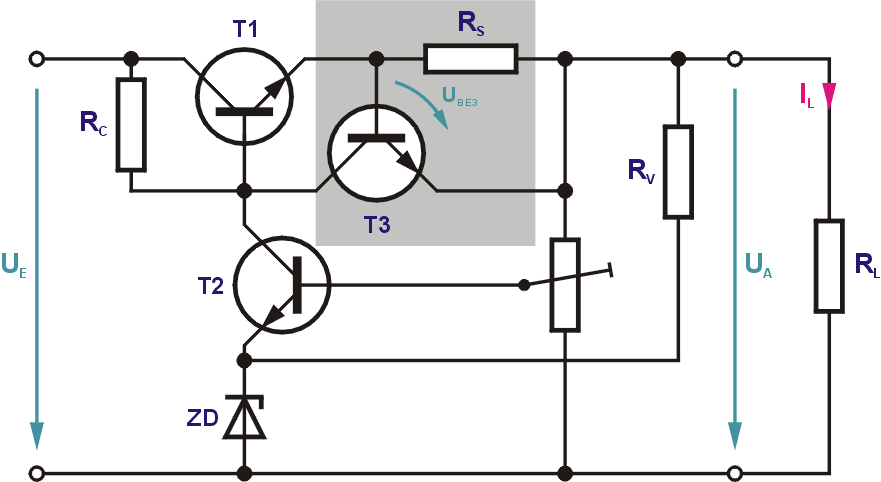
R_S muss so bemessen sein, dass beim maximal zulässigen Laststrom der Spannungsabfall den Wert der Schwellspannung der Basis-Emitter-Diode von T3 erreicht. T3 wird dann leitend und überbrückt die Basis-Emitter-Strecke von T1, woraufhin dieser zusteuert. Im Kurzschlussfall liegt über T1 die gesamte Eingangsspannung, was bei der Dimensionierung zu beachten ist.

Integrierte Spannungsregler
Auch in der Stromversorgung haben integrierte Schaltungen Einzug gehalten. Das macht den Aufbau eines stabilisierten Netzteils wesentlich einfacher. Die ersten Versionen hatten noch feste Spannungswerte. Wesentlich flexibler waren die Nachfolger mit einstellbarer Ausgangsspannung. Besonders beliebt war und ist der LM317 bzw. die DDR-Version B3170. Mit ihnen können ohne viel Aufwand Netzteile mit +1,2V ... +37V Ausgangsspannung und Ausgangsströmen von maximal 1,5A aufgebaut werden. Für negative Spannungen stehen die komplementären Typen B3370/LM337 zur Verfügung. Außerdem gibt es noch zwei "Hochvolt"-Typen, den Positivregler B3171 mit bis zu +57V Ausgangsspannung und den Negativregler B3371 mit maximal -47V. Die Schaltkreise sind gegen Übertemperatur und Kurzschluss gesichert. Unten zu sehen sind die Grundschaltungen laut Datenblatt.

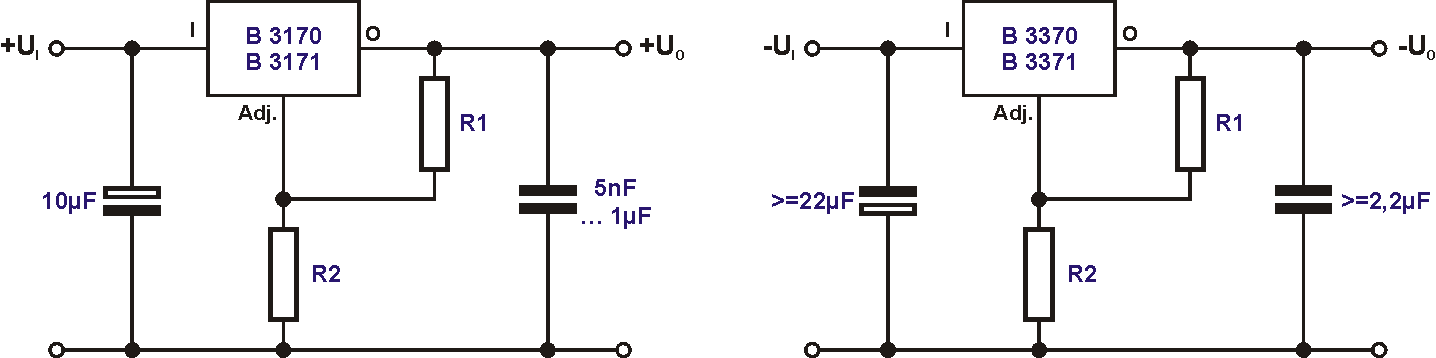
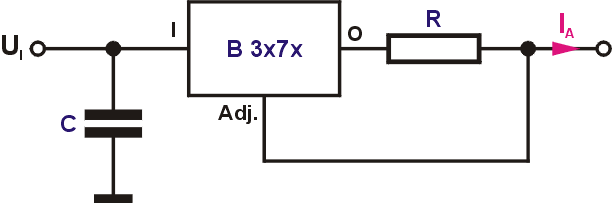
Am Einstellanschluss (Adj.) liegt eine Referenzspannung von rund 1,25V. Der empfohlene Wert für R1 ist 240Ω. Mit R2 kann die Spannung variiert werden, da die Ausgangsspannung die Summe aus der Referenzspannung und der Spannung über R2 ist. $$|U_O| = |U_{Ref}| \cdot \Big( 1 + \frac{R_2}{R_1}\Big) + |I_{ADJ}| \cdot R_2$$ Folgende Daten und Grenzwerte sind bei der Verwendung der Baureihe B3x7x noch zu beachten:
Maximale Verlustleistung: 15W;
Minimale Eingangs-/Ausgangs-Spannungsdifferenz: 3V;
minimaler Ausgangsstrom: 10mA;
Maximaler Strom aus dem Einstellanschluss: ≤ 100μA (typisch: 50μA).

B3x7x als Stromquelle
Die integrierte Schaltung lässt sich auch als einfache Stromquelle "missbrauchen". Da sich zwischen Ausgang und dem Einstellanschluss immer die Referenzspannung von etwa 1,25V einstellt, fließt ein konstanter Strom durch den Widerstand am Ausgang, den man ganz einfach mit dem ohmschen Gesetz berechnen kann. $$R = \frac{1,25V}{I_A}$$

< Startseite <   > nächste Seite >